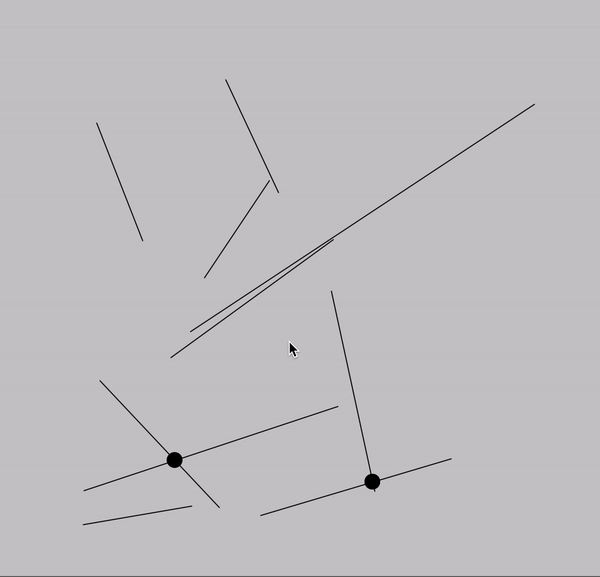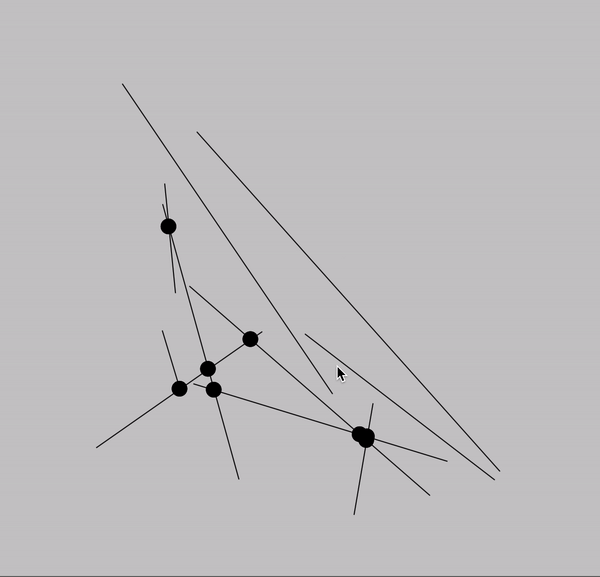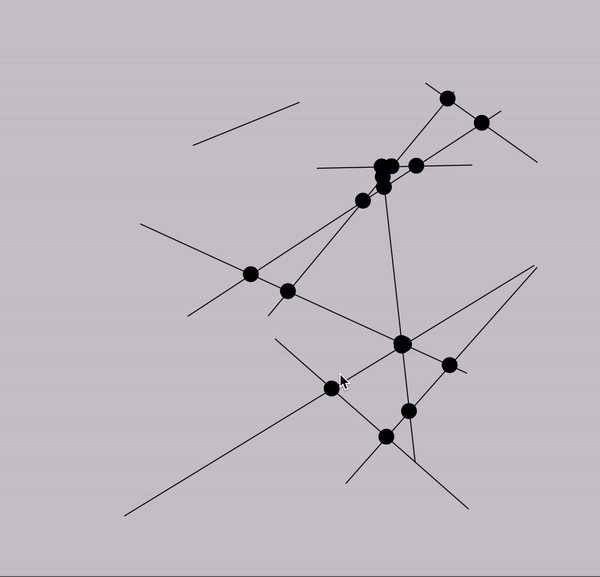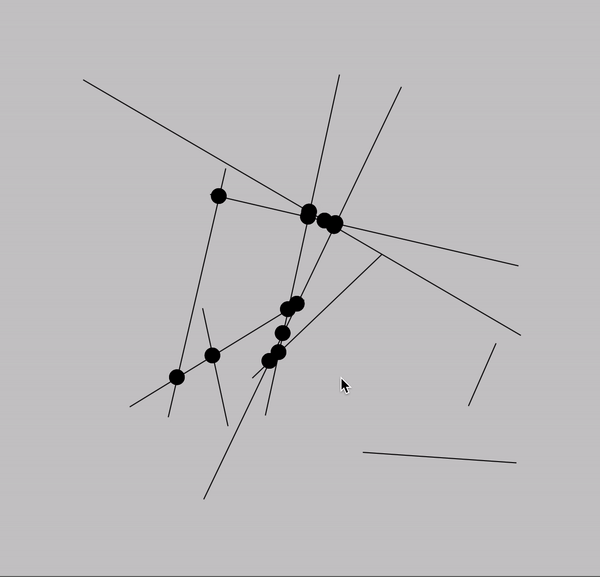
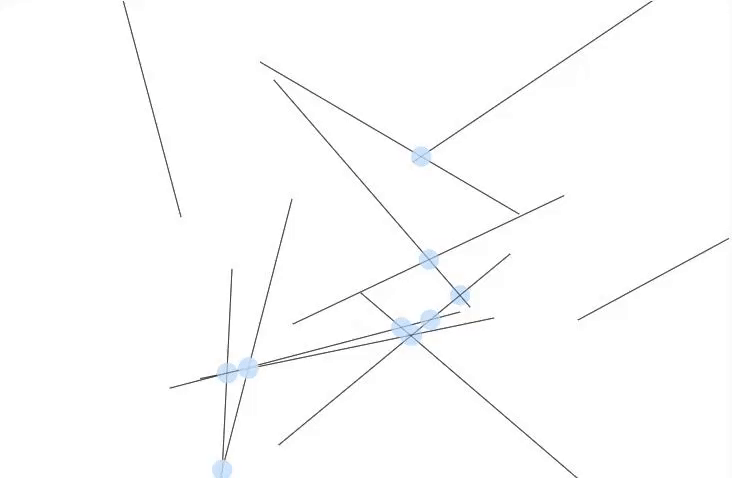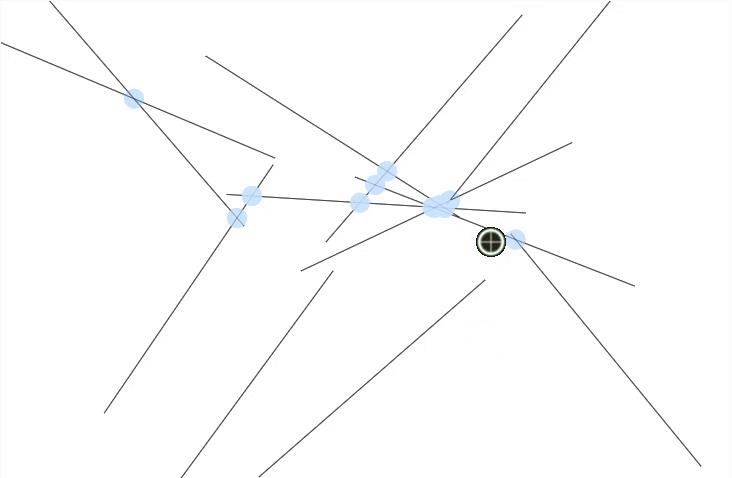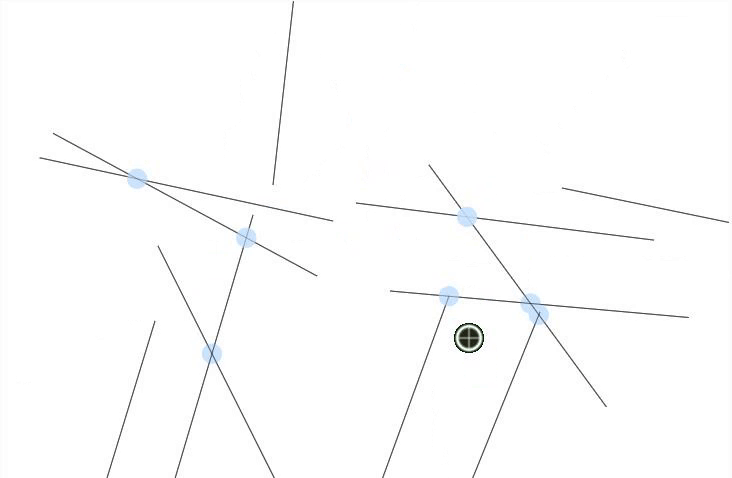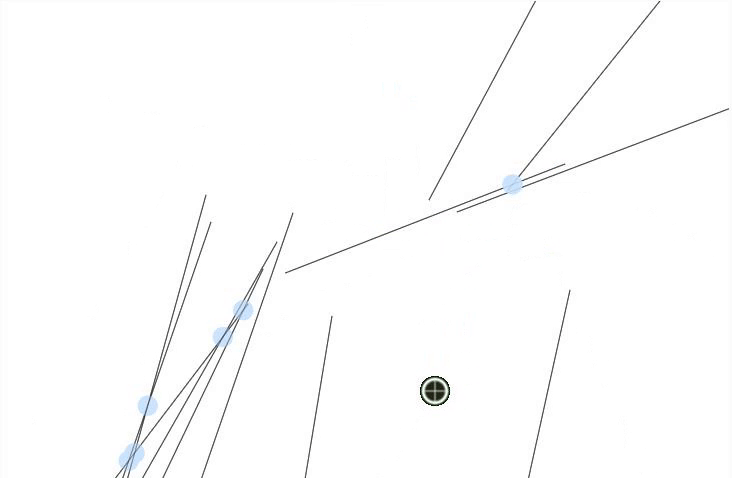
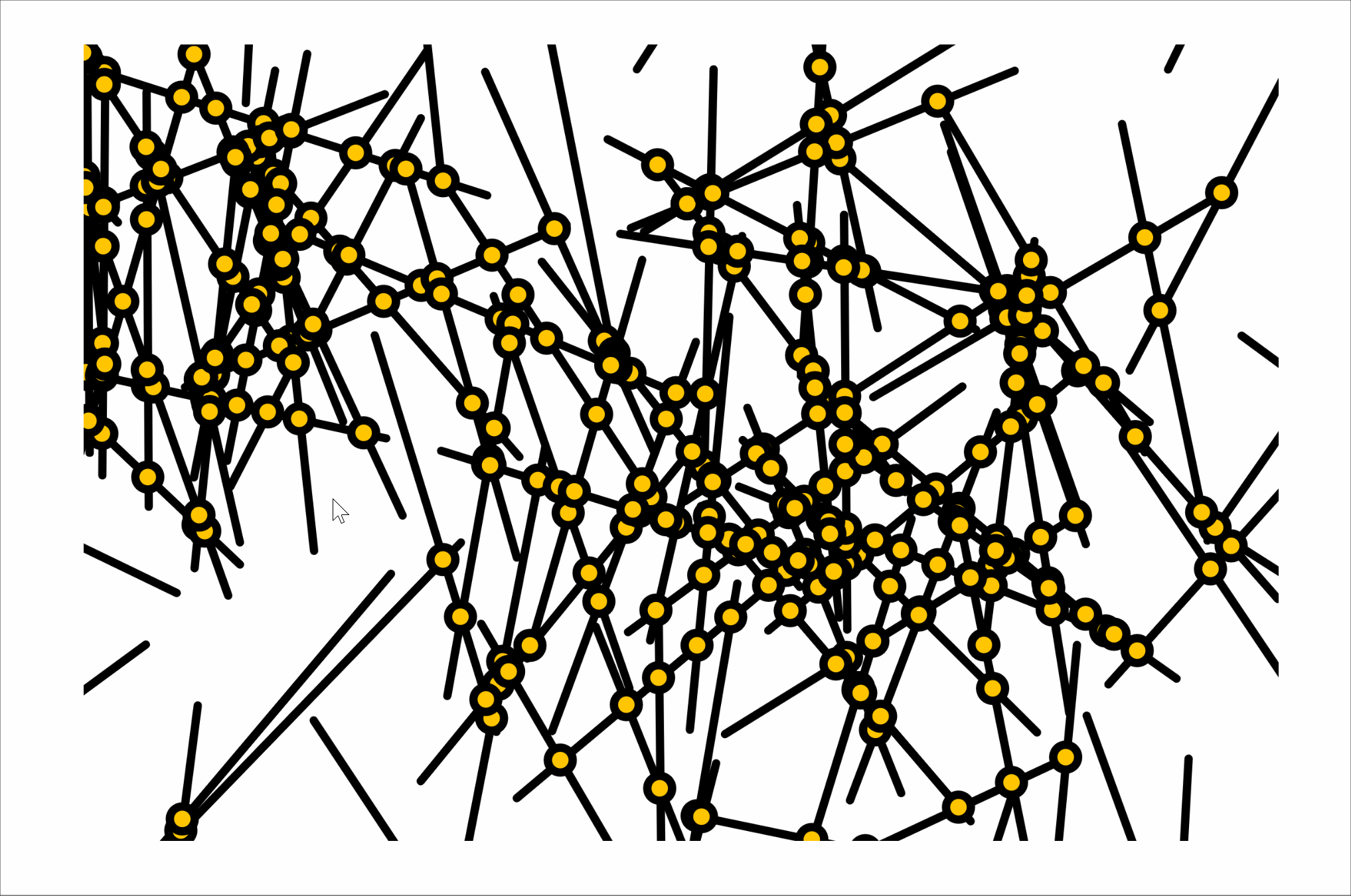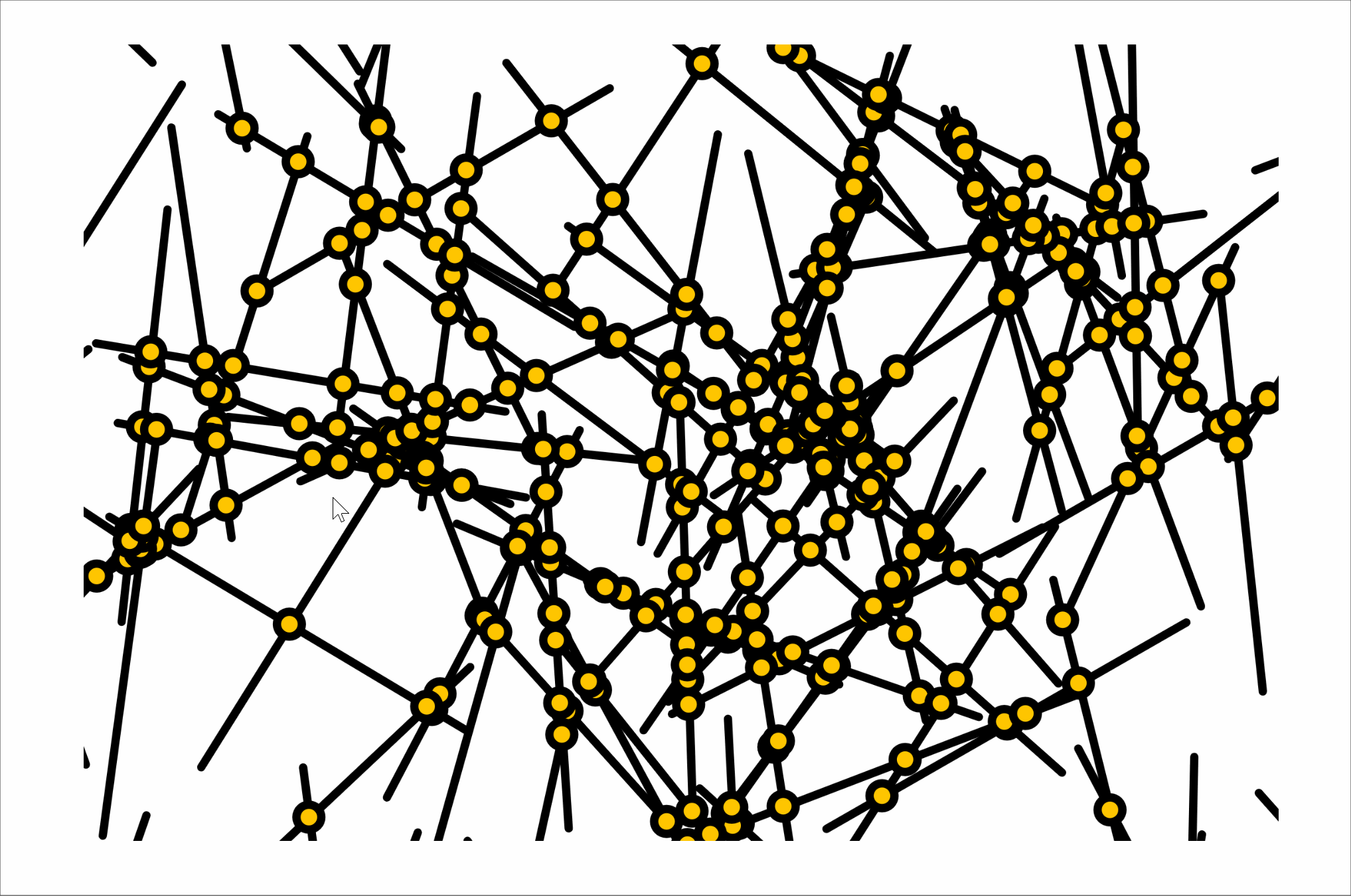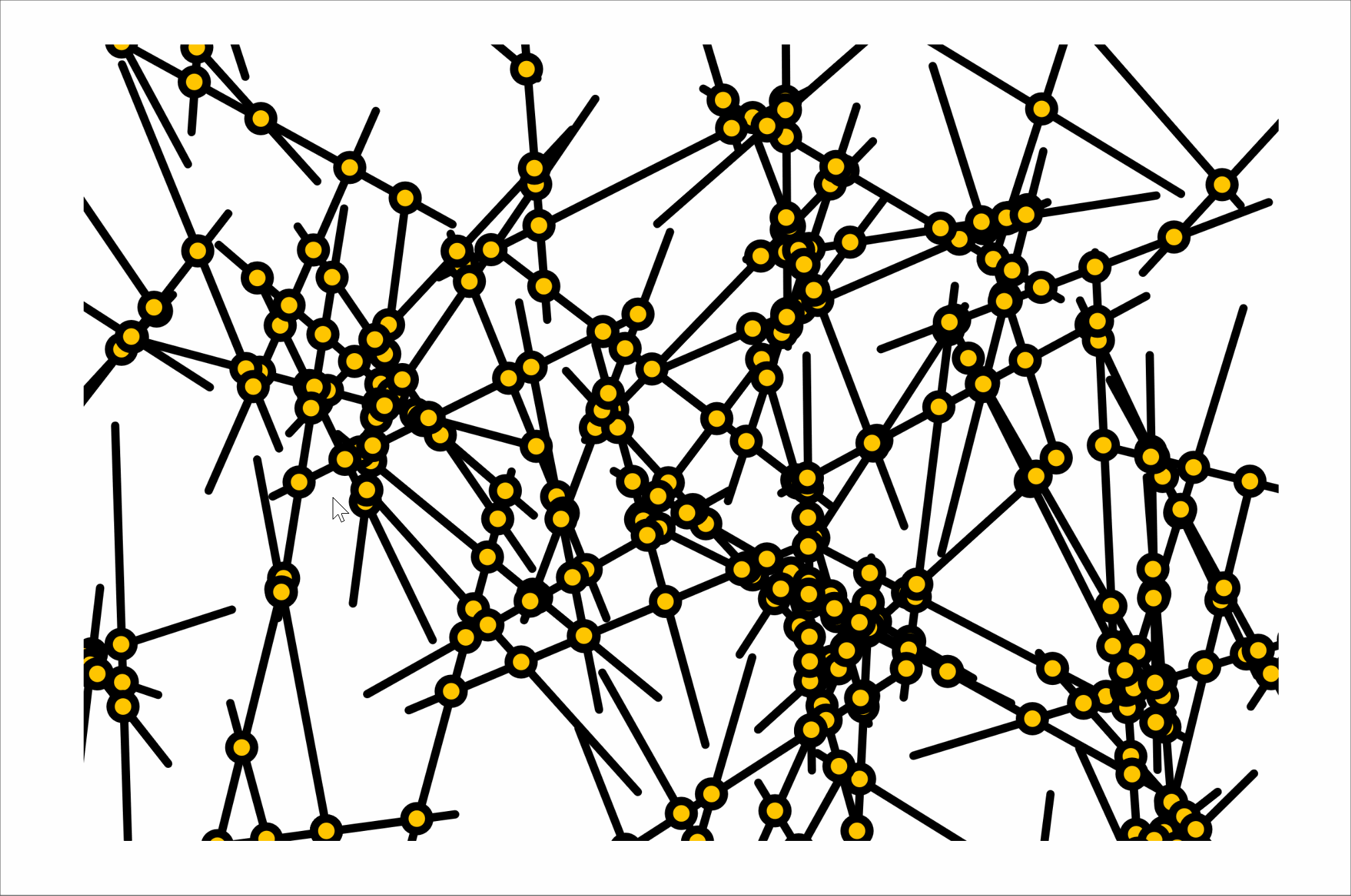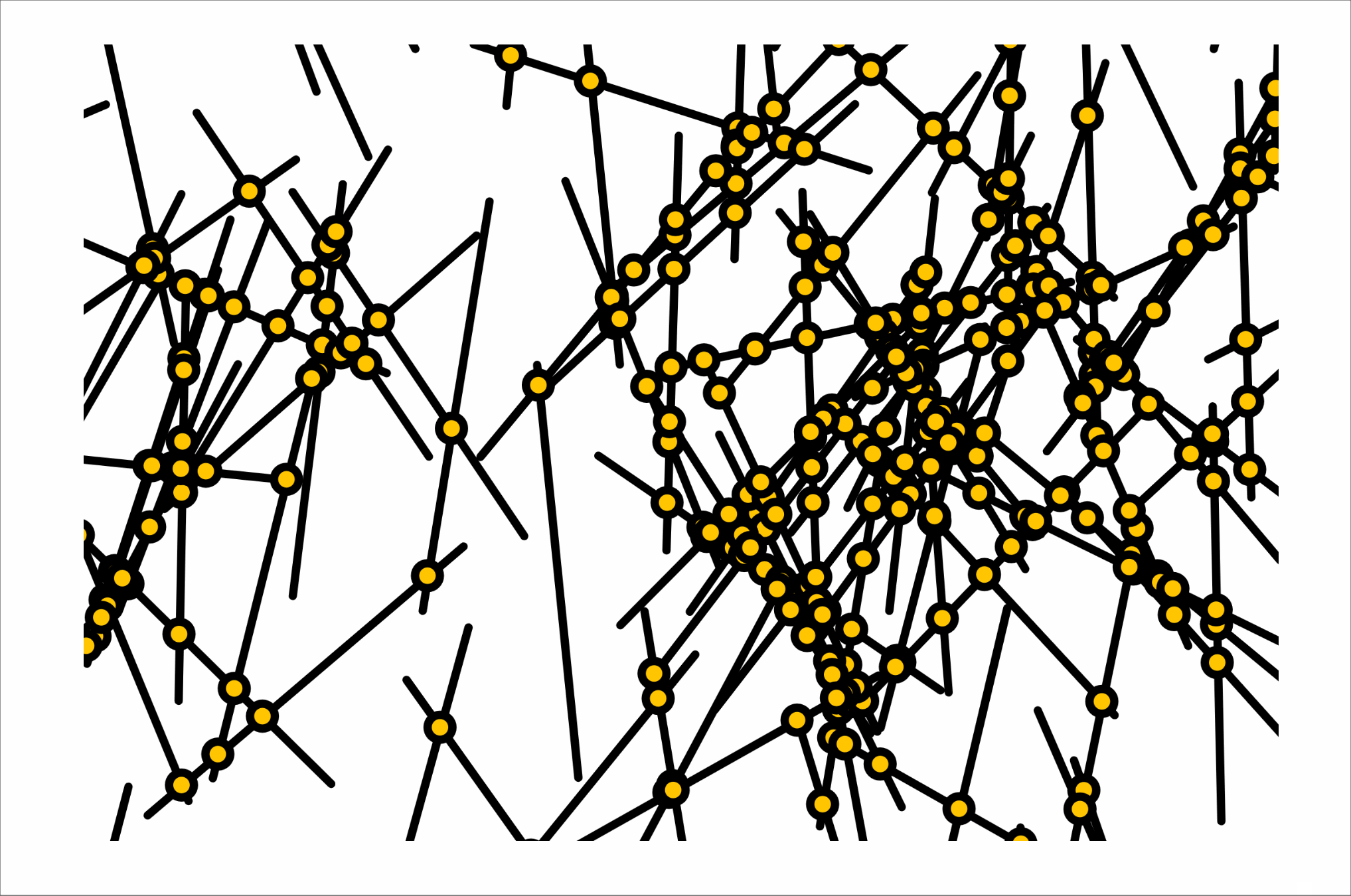
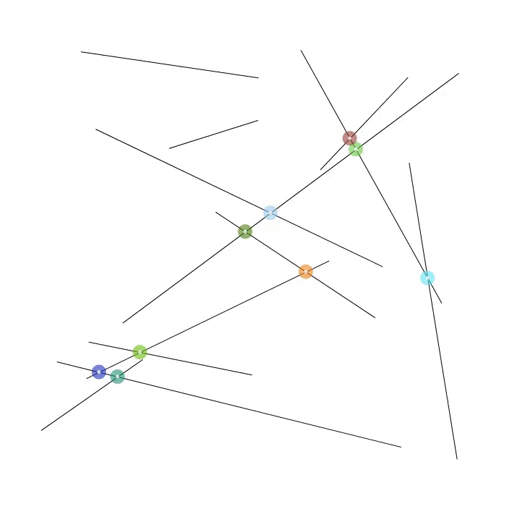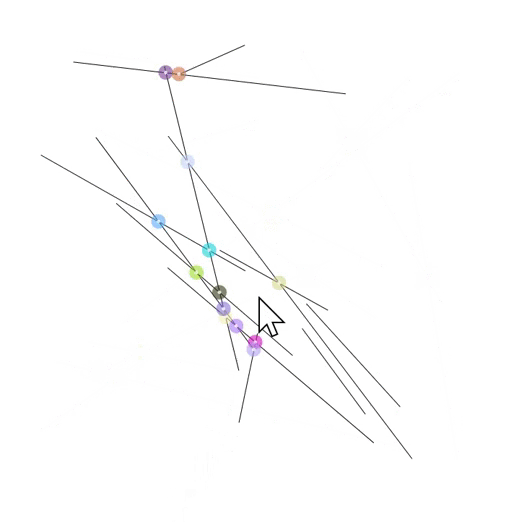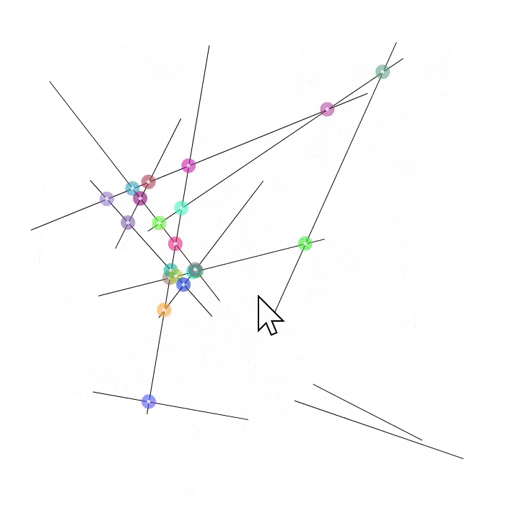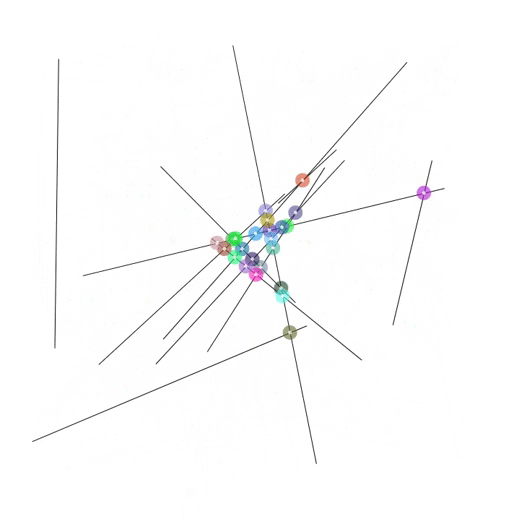
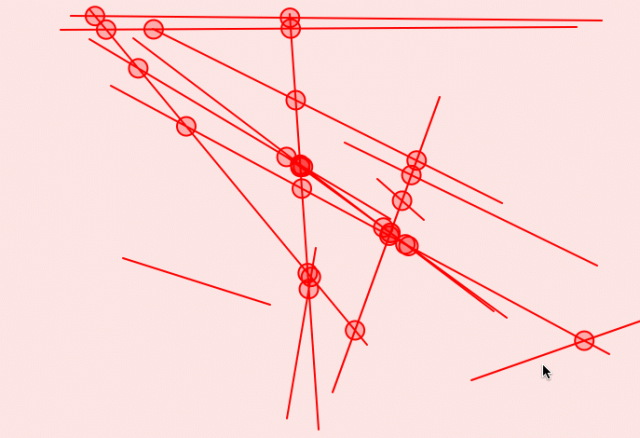
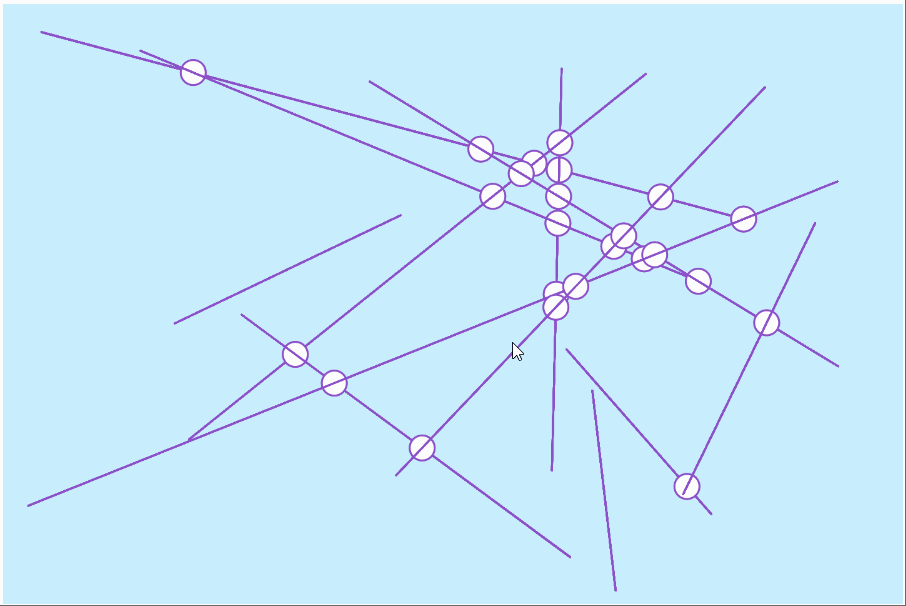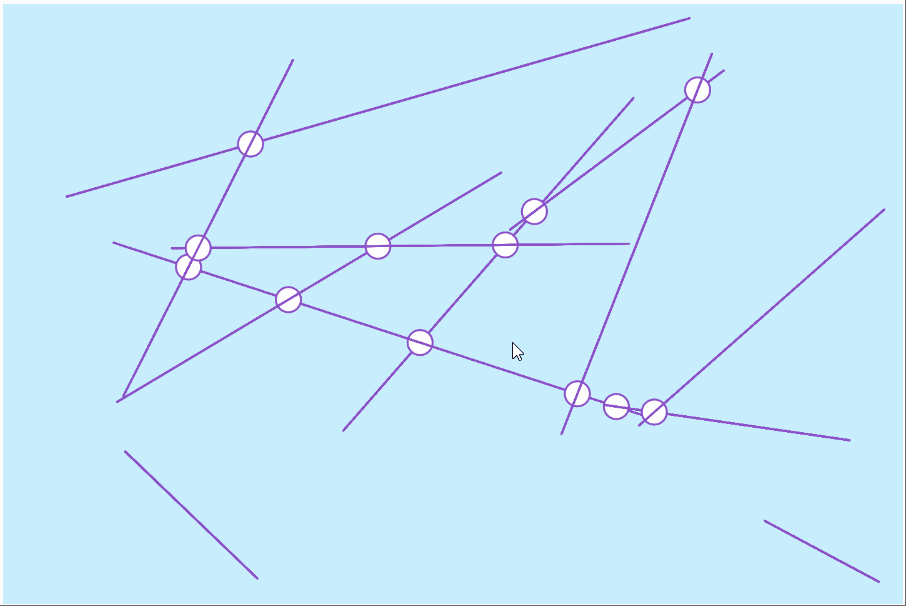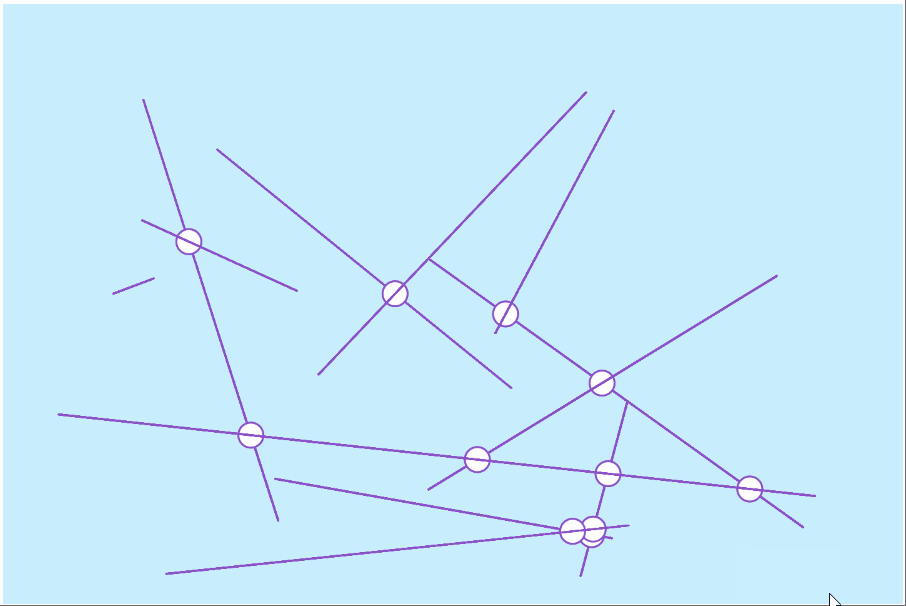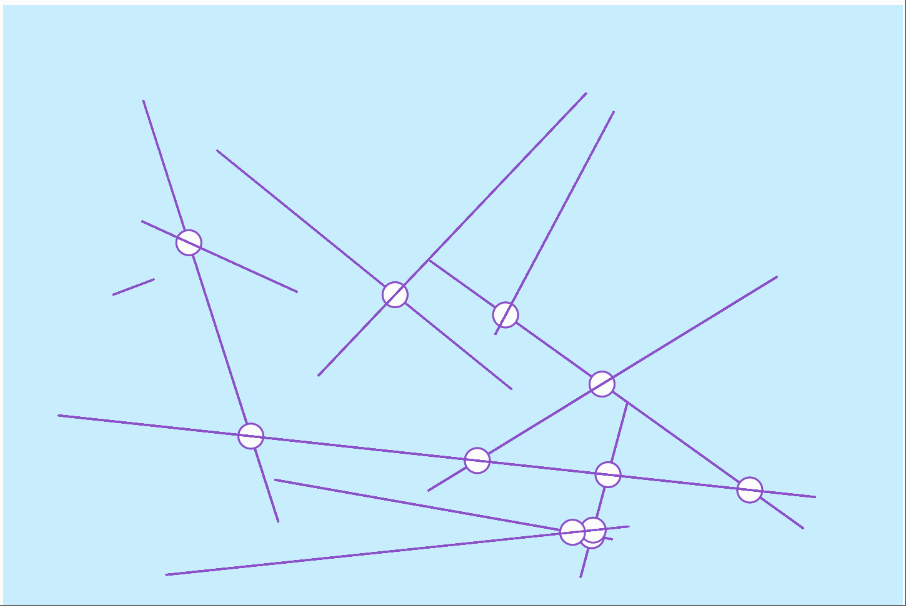
intersections
twelve intersections

seventy intersections

var lines = [];
var numOfLines = 12;
var intersectXArray =[];
var intersectYArray = [];
var yAxis = 1;
var c1, c2, c3;
function setup() {
createCanvas(720, 480);
background(0);
c1 = color(0);
c2 = color(16, 45, 117);
c3 = color(244, 89, 66);
// gradient background 1
setGradient(0, 0, windowWidth, windowHeight / 2, c1, c2, yAxis);
// gradient background 2
setGradient(0, windowHeight/2, windowWidth, windowHeight, c2, c3, yAxis);
for (var i = 0; i < numOfLines; i++) {
lines.push(new Line());
}
}
function draw() {
for (var i = 0; i < lines.length; i++) {
lines[i].display();
}
for (var i = 0; i < lines.length; i++) {
for (var j = 0; j < lines.length; j++) {
intersectXArray.push(intersect(lines[i].x1, lines[i].y1, lines[i].x2, lines[i].y2, lines[j].x1, lines[j].y1, lines[j].x2, lines[j].y2).x);
intersectYArray.push(intersect(lines[i].x1, lines[i].y1, lines[i].x2, lines[i].y2, lines[j].x1, lines[j].y1, lines[j].x2, lines[j].y2).y);
}
}
// display twinkling stars as intersection points
for (var i = 0; i < intersectXArray.length; i++) {
star = new Star(intersectXArray[i], intersectYArray[i]);
star.display();
star.twinkle();
}
}
function mousePressed() {
lines = [];
intersectXArray = [];
intersectYArray = [];
setup();
}
function Line() {
this.x1 = random(0, width);
this.y1 = random(0, height);
this.x2 = random(0, width);
this.y2 = random(0, height);
this.display = function() {
stroke(249, 252, 232, 20);
strokeWeight(1);
line(this.x1, this.y1, this.x2, this.y2);
}
}
function Star(x,y) {
this.x = x;
this.y = y
this.r = random(8);
this.display = function() {
stroke(22, 71, 119);
fill(255);
this.rc = constrain(this.r, 0, 9);
ellipse(this.x, this.y, this.rc, this.rc);
};
this.twinkle = function() {
if (this.r < 3) {
this.r += random(-.5,1.5);
} else if (this.r >= 3 && this.r < 6) {
this.r += random(-1,1);
} else if (this.r >=6 && this.r <=9) {
this.r += random(-1.5,0.5);
}
}
}
// creates gradients
function setGradient(x, y, w, h, c1, c2, axis) {
noFill();
if (axis == yAxis) { // Top to bottom gradient
for (var i = y; i <= y+h; i++) {
var inter = map(i, y, y+h, 0, 1);
var c = lerpColor(c1, c2, inter);
stroke(c);
line(x, i, x+w, i);
}
}
}
//from Paul Bourke http://paulbourke.net/geometry/pointlineplane/javascript.txt
function intersect(x1, y1, x2, y2, x3, y3, x4, y4) {
// Check if none of the lines are of length 0
if ((x1 === x2 && y1 === y2) || (x3 === x4 && y3 === y4)) {
return false
}
denominator = ((y4 - y3) * (x2 - x1) - (x4 - x3) * (y2 - y1))
// Lines are parallel
if (denominator === 0) {
return false;
}
let ua = ((x4 - x3) * (y1 - y3) - (y4 - y3) * (x1 - x3)) / denominator;
let ub = ((x2 - x1) * (y1 - y3) - (y2 - y1) * (x1 - x3)) / denominator;
// is the intersection along the segments
if (ua < 0 || ua > 1 || ub < 0 || ub > 1) {
return false
}
// Return a object with the x and y coordinates of the intersection
let x = x1 + ua * (x2 - x1)
let y = y1 + ua * (y2 - y1)
return {x, y}
}