Lasercut 2.0 – Cracks

./wp-content/uploads/sites/2/2013/10/cracks3.pdf

The results:

I changed my idea for the lasercut after the lecture today. Because of the limitations on shapes you can make with the lasercut, I decided to go back to using simple lines. I remembered back to the Recursive Trees code in the book Form + Code by Casey Reas and decided to search around the internet for similar code. Most trees had the problem of intersecting lines that would be impractical to lasercut. I was also thinking about the instructional art we had to engineer in an earlier assignment, because it was able to stop drawing lines once it detected another line.

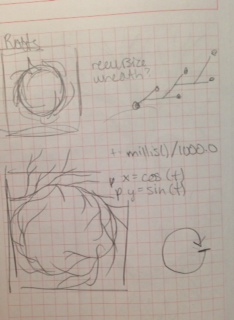
Then I was looking at particle systems on OpenProcessing and found this one code called “Roots” that uses nodes like particles, and creates new nodes based on their distance from other nodes. His inspiration was Rapidly-exploring Random Trees (RRT). The link to that person’s code is here: https://openprocessing.orgsketch/38518

So I thought that would be very applicable to a lasercut, where everything has to be intact. I studied and grossly simplified the code to the point where I could understand it and modeled the growth of the nodes to match the Lissajous curves we learned in class. (Although, the circle still looked the best out of the various PDFs I saved…)

Here are my sketches:

Unfortunately, my code doesn’t work in Javascript so I can’t show it on OpenProcessing, but it is below:

// Credit goes to Alexander Mordvintsev for his code "Roots"
// which was inspired by RRT (Rapidly-exploring Random Trees)
// See here: https://openprocessing.orgsketch/38518

import processing.pdf.*;

ArrayList nodes;
int     branching    = 100;
float   branchLength = 5.0;
 
void setup()
{
  size(500,500);
  background(255);
  strokeWeight(1);
  smooth();
  nodes = new ArrayList();
  beginRecord(PDF, "cracks1.pdf");
}

void draw() {
  // Adds the parent node
  if (nodes.size() == 0)
    nodes.add(new Node(width-20,height/2));
  // Accelerates the amount of growth per frame
  for (int i=0; i<10; i++)
    grow();
}

void keyPressed() {
  endRecord();
  exit();
}

Node findNearest(Node p) {
  float minDist = 1e10;
  int minIndex  = -1;
  for (int i=0; i sq(branching));
  x += px;
  y += py;
  
  // Boundaries for the frame of the lasercut
  if(x>20 && x20 && y= branchLength) {
      Node newNode = new Node(base, sample);
      nodes.add(newNode);
      newNode.display();
    }
  }
}

class Node
{
  PVector pos;
  Node parent;
 
  Node(float x, float y) {
    pos = new PVector(x,y);
  }
  
  Node(Node base, Node sample) {
    PVector step = PVector.sub(sample.pos,base.pos);
    step.limit(5.0);
    pos = PVector.add(base.pos,step);
    parent = base;
  }
 
  float dist(Node other) {
    return PVector.dist(pos,other.pos);
  }
  
  // Draws a line between nearest node and new node
  void display() {
    if (parent!=null) {
      line(parent.pos.x, parent.pos.y, pos.x, pos.y);
    }
  }
}