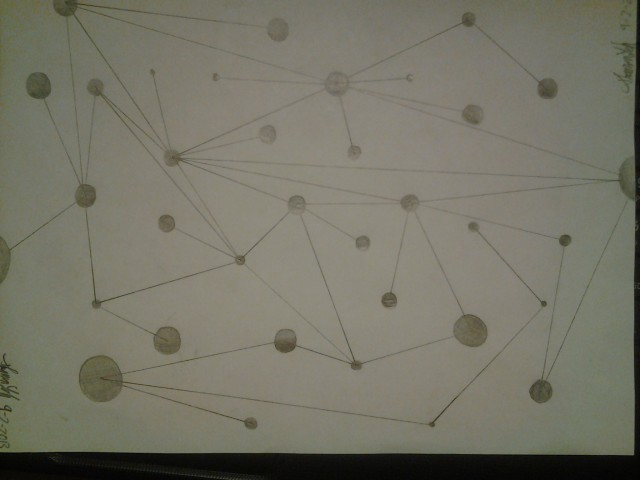
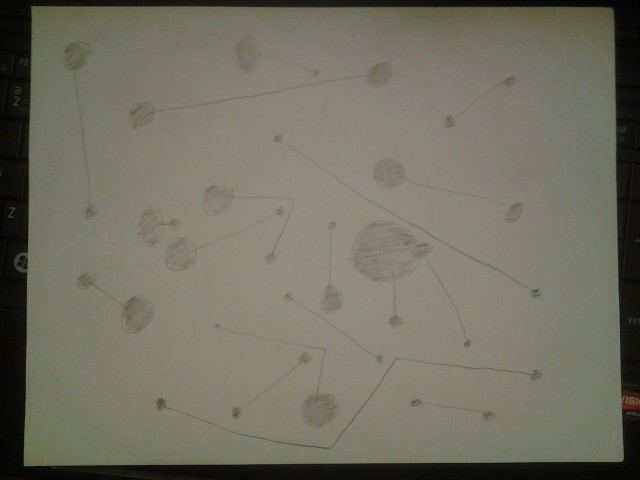
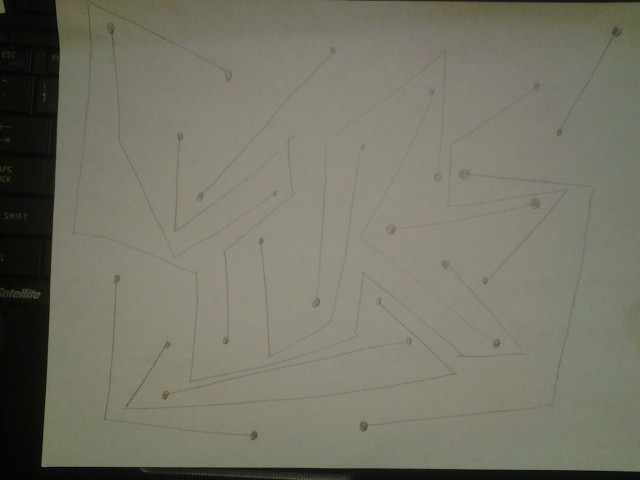
Instructional Drawing

1. Draw 36 small circles randomly scattered on the paper. Fill in the circles.
2. Pick 2 random circles such that neither is connected. Draw a path between them such that
– the path does not cross any existing paths nor circles
– the path consists of only connected line segments
– the path consists of fewest number of line segments possible
3. Repeat step 2 until there are no unconnected circles left.

Here are the 3 results:

I should have specified that the circles don’t overlap. The circles should also be paired up to be connected to each other and not any other circles. I considered describing the circles as “lone nodes” (for my fellow comp sci majors) in step 2, but decided against it last minute. Now I think I should have included that part after all. The pairs of circles should be chosen at random, but it seems like they all mostly chose the pairs to be close-by circles to draw straight lines with.

The 3 samples ended up looking like constellations, which was unintended, but pretty cool. I found it amusing how they all put in effort to make each circle interesting (note those 3-D shading).

My initial draft (with fewer circles), was inspired by circuit boards, in case you’re curious.