1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| var boolDoRefresh;
const CANV_HEIGHT = 720;
const CANV_WIDTH = 720;
const H_MARGIN = CANV_WIDTH / 14;
const V_MARGIN = CANV_HEIGHT / 14;
const V_NUM_LINES = 56;
const H_NUM_LINES = 56;
const H_UNIT_SIZE = (CANV_WIDTH - (H_MARGIN * 2)) / H_NUM_LINES;
const V_UNIT_SIZE = (CANV_HEIGHT - (V_MARGIN * 2)) / V_NUM_LINES;
const LINE_LENGTH = H_UNIT_SIZE * 2;
const HORIZONTAL_FREQ = 0.25;
function setup() {
createCanvas(720, 720);
background('#EEEEEE');
strokeWeight(0.75);
boolDoRefresh = true;
}
function draw() {
if(boolDoRefresh) {
background('#EEEEEE');
constructLines();
boolDoRefresh = false;
}
}
function mousePressed() {
boolDoRefresh = true;
}
function constructLines() {
var angleOff = random(0.2);
var gapX = random(0.5);
var gapY = random(0.5);
var gapScale = 0.15;
noiseSeed(random(100));
var horizontal = random(1);
for(var i = 0; i < H_NUM_LINES; i++) {
for(var j = 0; j < V_NUM_LINES; j++) {
angleOff += 0.1;
gapX += i * gapScale;
gapY += j * gapScale;
if(noise((i * gapScale), (j * gapScale)) > 0.25) {
var angle = random(noise(angleOff) * 90);
centerLine(H_MARGIN + i * H_UNIT_SIZE, V_MARGIN + j * V_UNIT_SIZE, LINE_LENGTH, angle, horizontal);
}
}
}
}
function centerLine(x, y, length, angle, horizontal) {
angleMode(DEGREES);
var randNum = random(2);
var x1 = x + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? cos(angle) : sin(angle)));
var y1 = y + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? sin(angle) : cos(angle)) * (randNum > 1 ? 1 : -1));
var x2 = x - ((length / 2) * (horizontal < HORIZONTAL_FREQ ? cos(angle) : sin(angle)));
var y2 = y + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? sin(angle) : cos(angle)) * (randNum > 1 ? -1 : 1));
line(x1, y1, x2, y2);
} |
var boolDoRefresh;
const CANV_HEIGHT = 720;
const CANV_WIDTH = 720;
const H_MARGIN = CANV_WIDTH / 14;
const V_MARGIN = CANV_HEIGHT / 14;
const V_NUM_LINES = 56;
const H_NUM_LINES = 56;
const H_UNIT_SIZE = (CANV_WIDTH - (H_MARGIN * 2)) / H_NUM_LINES;
const V_UNIT_SIZE = (CANV_HEIGHT - (V_MARGIN * 2)) / V_NUM_LINES;
const LINE_LENGTH = H_UNIT_SIZE * 2;
const HORIZONTAL_FREQ = 0.25;
function setup() {
createCanvas(720, 720);
background('#EEEEEE');
strokeWeight(0.75);
boolDoRefresh = true;
}
function draw() {
if(boolDoRefresh) {
background('#EEEEEE');
constructLines();
boolDoRefresh = false;
}
}
function mousePressed() {
boolDoRefresh = true;
}
function constructLines() {
var angleOff = random(0.2);
var gapX = random(0.5);
var gapY = random(0.5);
var gapScale = 0.15;
noiseSeed(random(100));
var horizontal = random(1);
for(var i = 0; i < H_NUM_LINES; i++) {
for(var j = 0; j < V_NUM_LINES; j++) {
angleOff += 0.1;
gapX += i * gapScale;
gapY += j * gapScale;
if(noise((i * gapScale), (j * gapScale)) > 0.25) {
var angle = random(noise(angleOff) * 90);
centerLine(H_MARGIN + i * H_UNIT_SIZE, V_MARGIN + j * V_UNIT_SIZE, LINE_LENGTH, angle, horizontal);
}
}
}
}
function centerLine(x, y, length, angle, horizontal) {
angleMode(DEGREES);
var randNum = random(2);
var x1 = x + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? cos(angle) : sin(angle)));
var y1 = y + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? sin(angle) : cos(angle)) * (randNum > 1 ? 1 : -1));
var x2 = x - ((length / 2) * (horizontal < HORIZONTAL_FREQ ? cos(angle) : sin(angle)));
var y2 = y + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? sin(angle) : cos(angle)) * (randNum > 1 ? -1 : 1));
line(x1, y1, x2, y2);
}
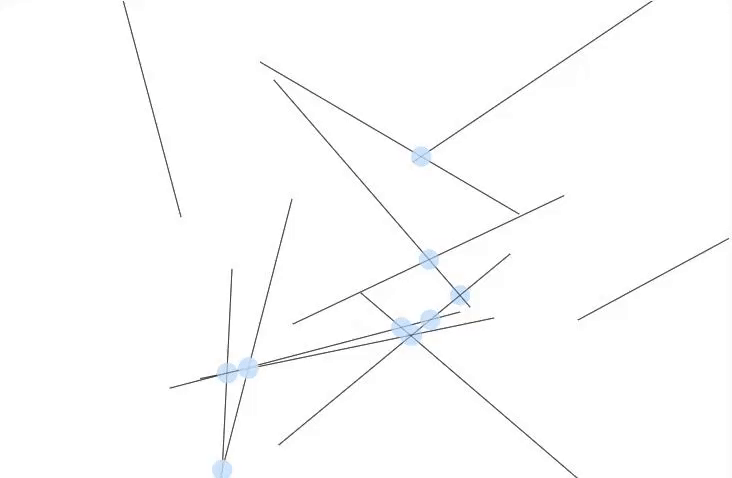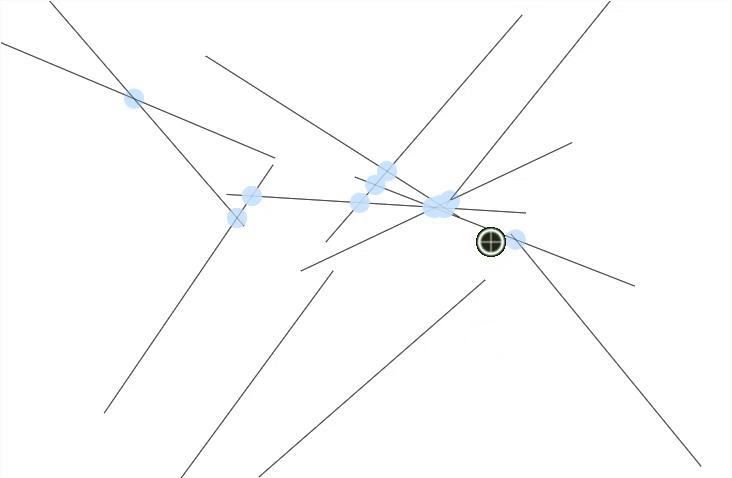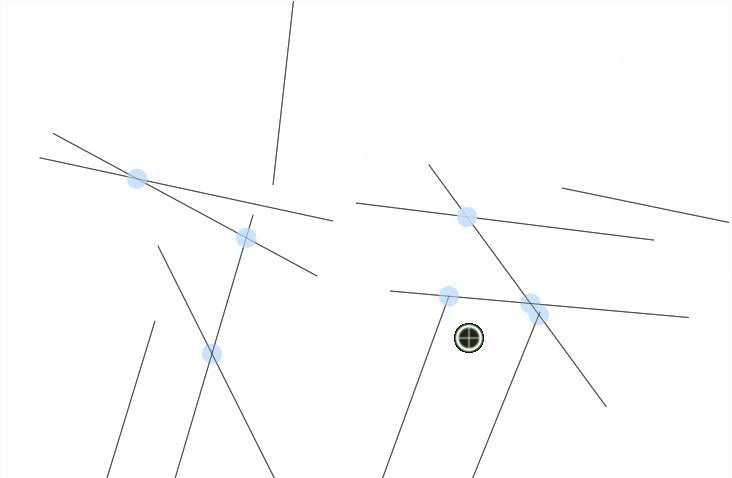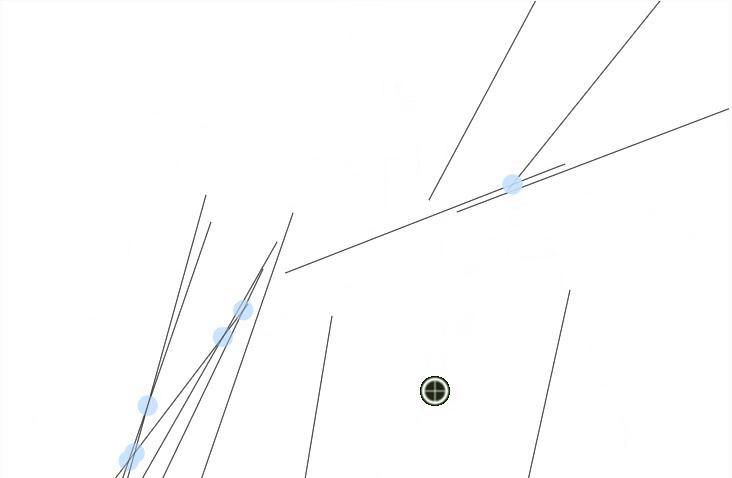
Process/Reflection:
I dedicated a significant amount of my work on this project to my observations of Vera Molnár's Interruptions. I noted the following:
- In each composition, all the lines are the same length.
- Each line's center falls into a 56x56 grid.
- Each line's length is twice the distance of the spacing on the grid (in other words, the endpoints of a fully vertical or horizontal line will intersect with the centerpoints of the lines immediately next to it)
- While the lines' angles are random, they tend to point in a vertical direction on three of Molnár's compositions and in a horizontal direction on one composition
- Not every line is present. There are gaps in each composition. While the location of the gaps seem random, missing lines tend to exist near other missing lines.
- Gaps appear fairly infrequently
- There is some slight variation in the background color, ranging from off-white to a mid-light grey.
- There is a margin around each composition. Not all of the compositions are centered, but the most centered composition leaves a margin of about 1/14th of the page around the composition.
As I was creating my own compositions in Javascript, I noticed that there was a considerable amount of care needed to produce a convincing randomness. I Perlin noise to create the gaps and the variation in line angles, something that did not exist in the time when the original compositions were created, to make a composition that was close to Molnár's. I think I was only mildly successful, though, as while the lines seem to have a similar character to the originals, the gaps do not. Their borders are too harsh and they are not quite the right shape. I think my line weight is a little off, as well.
Reproducing randomness is incredibly challenging without knowledge of the calculations that led to Molnár's compositions, and I now have a much greater appreciation for the work that goes into producing art with randomness as a factor.