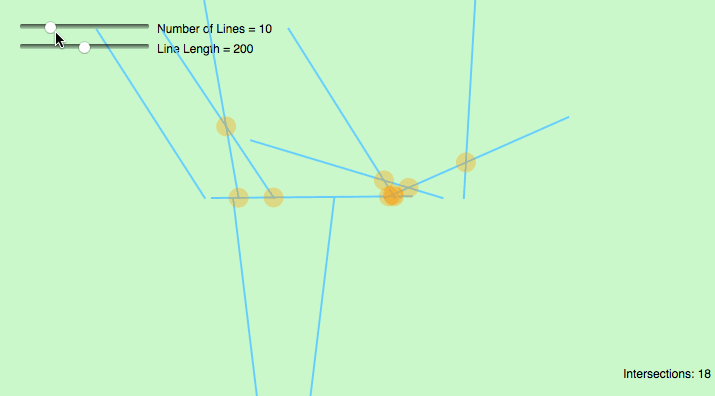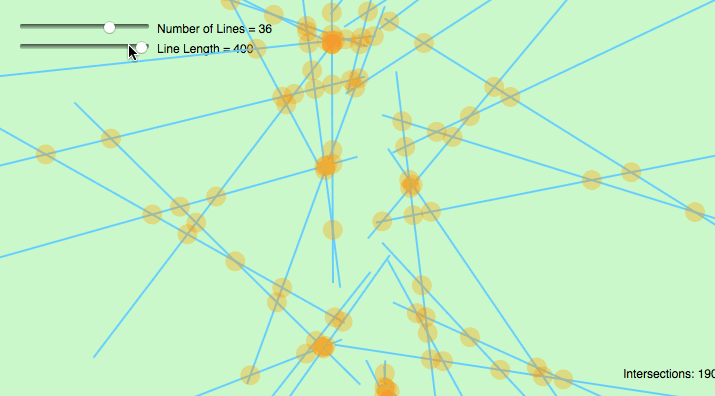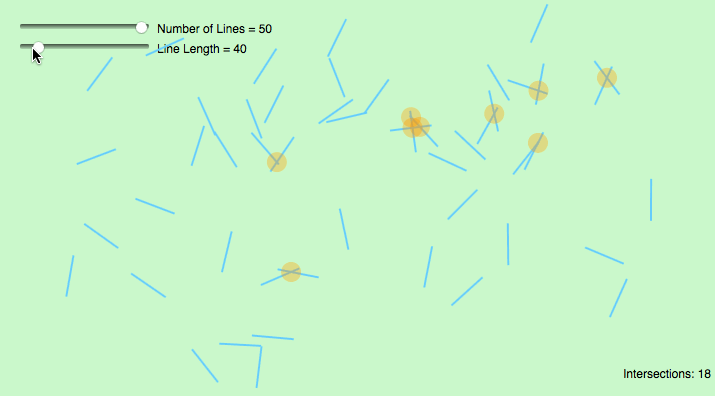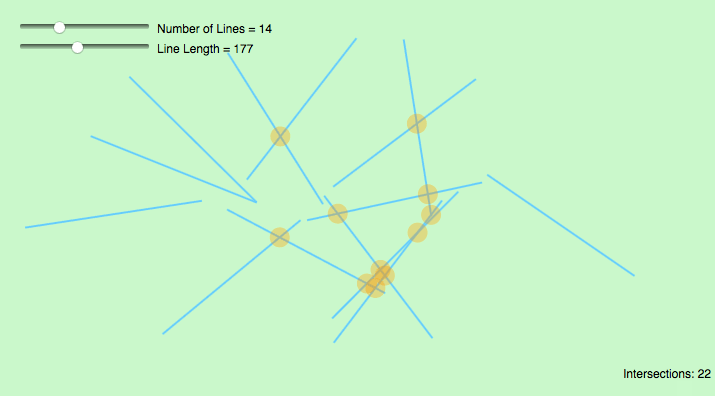
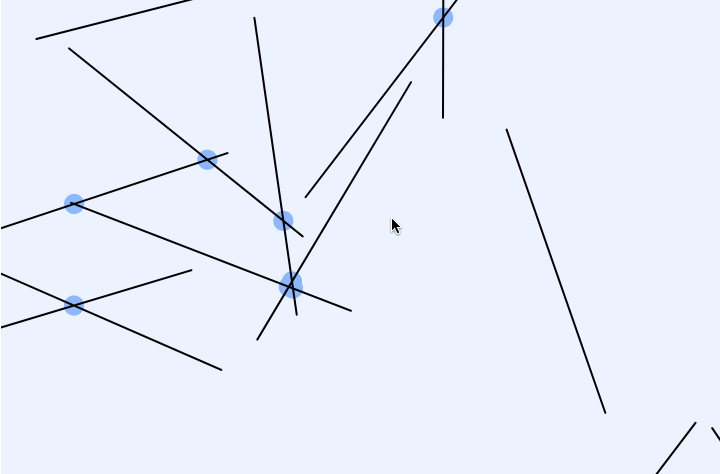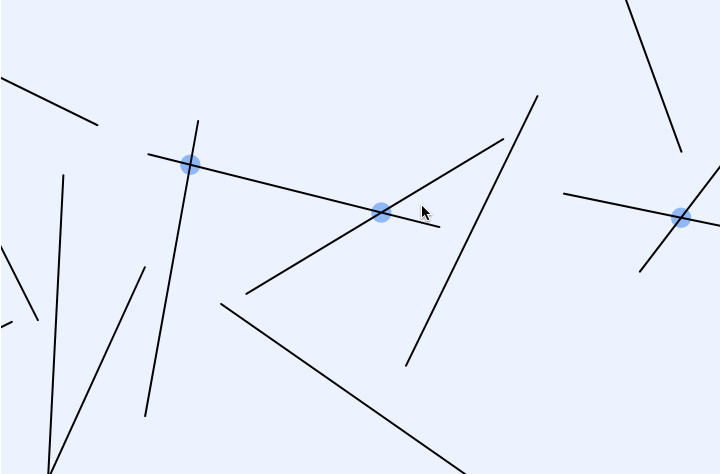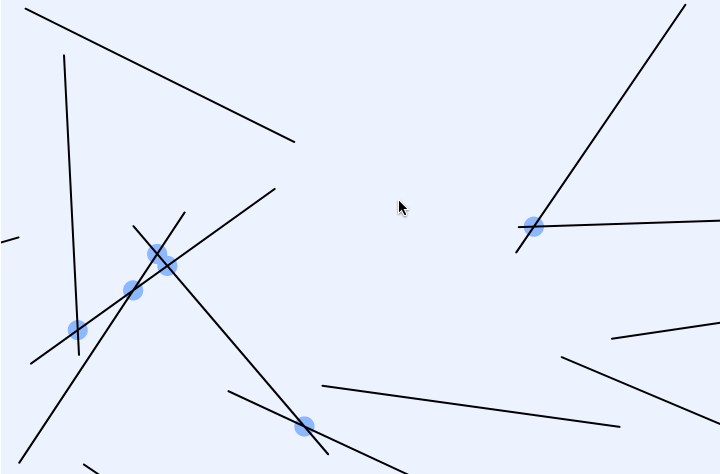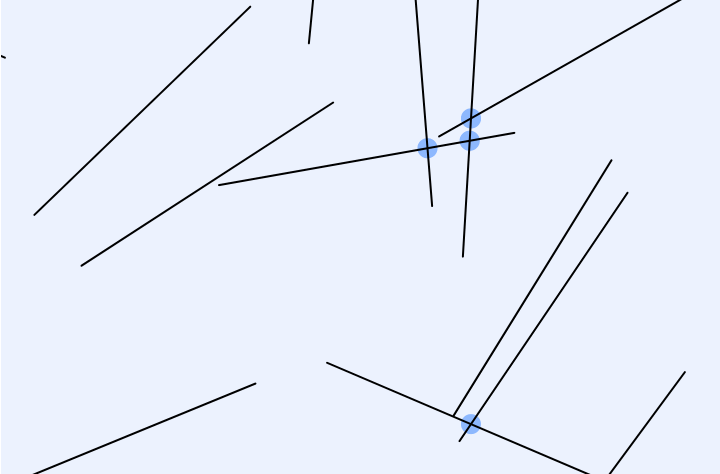
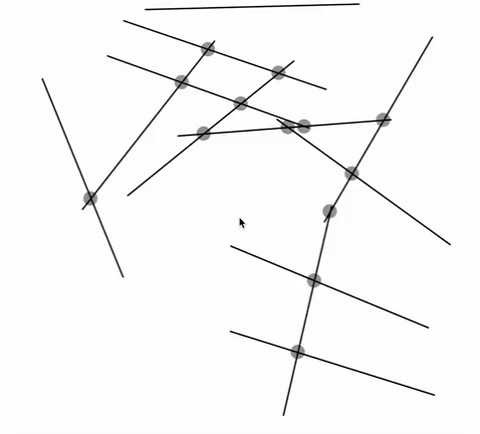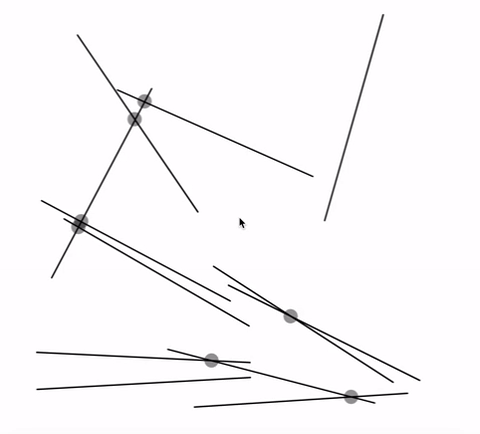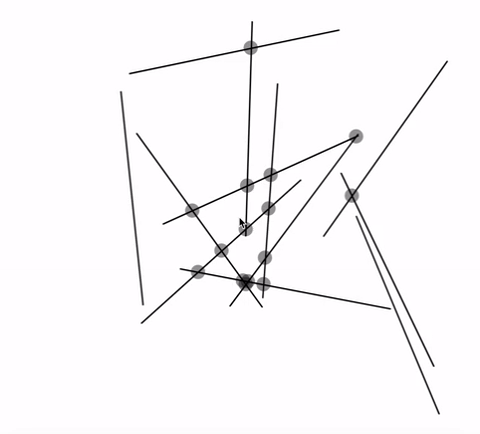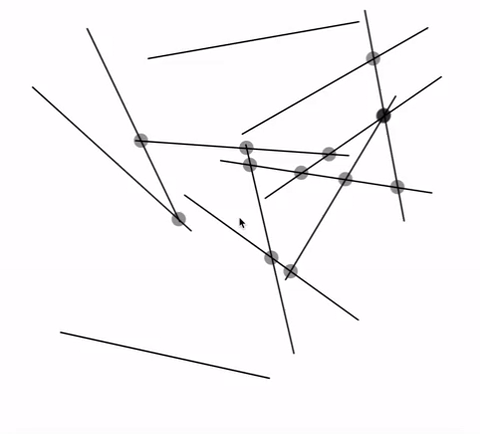
GIF:
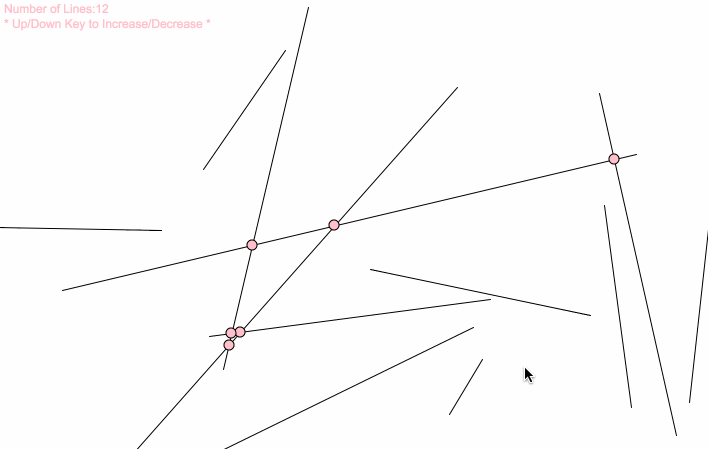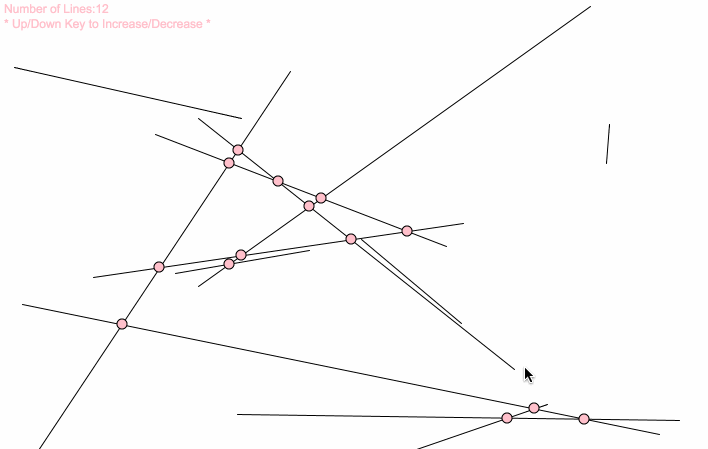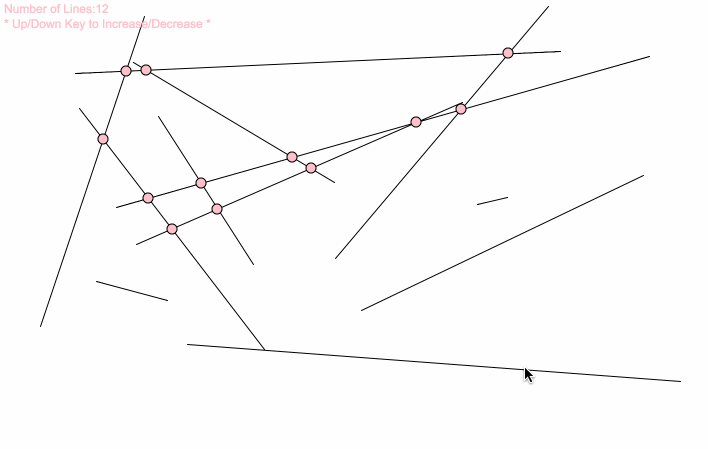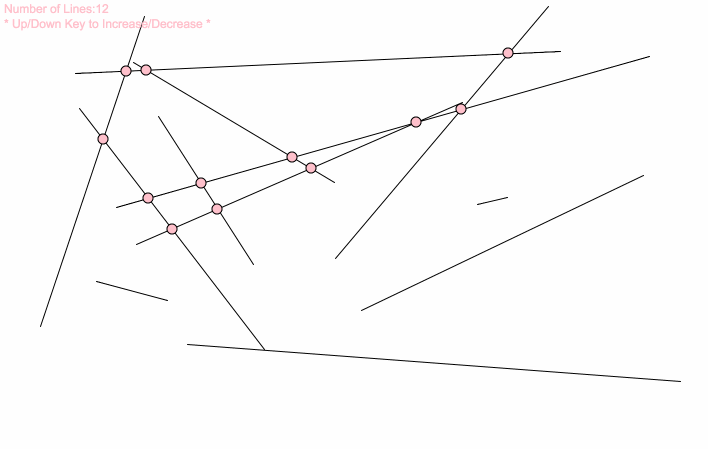
var lineNum = 12;//change this number to get more lines var lineSets = []; function setup() { createCanvas(720, 480); lineGenerator(); } function draw() { background(255); for (var j = 0; j < lineNum; j++){ var x1 = lineSets[j][0]; var y1 = lineSets[j][1]; var x2 = lineSets[j][2]; var y2 = lineSets[j][3]; line(x1, y1, x2, y2); for (var s = 0; s < lineNum; s++){ var x3 = lineSets[s][0]; var y3 = lineSets[s][1]; var x4 = lineSets[s][2]; var y4 = lineSets[s][3]; if (intersect(x1, y1, x2, y2, x3, y3, x4, y4) != false){ var cCenter = intersect(x1, y1, x2, y2, x3, y3, x4, y4); fill("pink"); ellipse(round(cCenter[0]), round(cCenter[1]), 10); } } } text("Number of Lines:" + lineNum, 10 ,20); text("* Up/Down Key to Increase/Decrease *", 10 ,35); } function mousePressed() { lineGenerator(); } function keyPressed() { if (keyCode === UP_ARROW) { lineNum += 1; lineGenerator(); } else if (keyCode === DOWN_ARROW) { lineNum -= 1; lineGenerator(); } } function lineGenerator(){ lineSets = []; for (var i = 0; i < lineNum; i++){ var x1 = round(random(0,width+1)); var y1 = round(random(0,height+1)); var x2 = round(random(0,width+1)); var y2 = round(random(0,height+1)); lineSets[i] = [x1, y1, x2, y2] } } // taken and modified from http://paulbourke.net/geometry/pointlineplane/javascript.txt // line intercept math by Paul Bourke http://paulbourke.net/geometry/pointlineplane/ // Determine the intersection point of two line segments // Return FALSE if the lines don't intersect function intersect(x1, y1, x2, y2, x3, y3, x4, y4) { // Check if none of the lines are of length 0 if ((x1 === x2 && y1 === y2) || (x3 === x4 && y3 === y4)) { return false } var denominator = ((y4 - y3) * (x2 - x1) - (x4 - x3) * (y2 - y1)) // Lines are parallel if (denominator === 0) { return false } var ua = ((x4 - x3) * (y1 - y3) - (y4 - y3) * (x1 - x3)) / denominator var ub = ((x2 - x1) * (y1 - y3) - (y2 - y1) * (x1 - x3)) / denominator // is the intersection along the segments if (ua < 0 || ua > 1 || ub < 0 || ub > 1) { return false } // Return a object with the x and y coordinates of the intersection var x = x1 + ua * (x2 - x1) var y = y1 + ua * (y2 - y1) return [x, y] } |