yuvian – Page 2 – 60212: INTERACTIVITY & COMPUTATION

yuvian-Scope

For my praxinoscope design, I chose to keep it simple. In order to create this sketch, I first conducted research on bezier vertices and objects in Java and learned how to implement them in this project. In this praxinoscope, I used two, pulsing hearts - inspired by this heart emoji because it's one of my favorite emojis ¯\_(ツ)_/¯.


void drawArtFrame (int whichFrame) { 

  // Draw the frame number
  fill(0); 
  noStroke(); 
  textAlign(CENTER, CENTER); 
  text (whichFrame, -1, -47);

  // Draw expanding double heart emojis
  int nHearts = 3;
  for (int i=0; i

yuvian-Interruptions

Observations:
- The artwork is square.
- The artwork consists of many short black lines, on a white background.
- The lines all have the same length.
- The artwork is basically composed of a 60 * 60 grid.
- Horizontal lines show up less frequently than vertical lines.
- Lines take up more than half of the space.

The most challenging part of this assignment was understanding Perlin noise. I've used it in the past but not much. The concept of noise and trigonometric functions in order to randomize the angles of the lines took a while for me to figure out. Something that I understood almost at once was the gridlike structure of Molnár's "Interruptions". I immediately noticed the 56X56 grid upon which the lines were fixed. I think I was generally successful at recreating the artist's work but my lines are not as randomized as the original. This is probably an easy fix as I would have to go back in and manipulate some of the variables within noise but for now, it is a close representation of Molnár's work. I appreciate how seemingly simple the original work appears at first when in actuality, it is a lot more complex than I had originally thought.

yuvian-Reading

The Critical Engineer recognises that each work of engineering engineers its user, proportional to that user's dependency upon it.

A critical engineer's work is understood to have an effect on its user corresponding to degree in which the user relies on it. Thus, the more a user depends on the work, the more they will be influenced by its content.

This is an interesting thought regarding the relationship between a product and its user/audience. I can see this belief reflected in popular culture regarding the prevalence of smartphones in our current society. It is often joked that as our phones become "smarter" we become less so. Nowadays, it is easy to see the influence technology has on our lives. Recently, research has shown the detrimental effects of blue light on our Circadian clock, our postures suffer due to long hours in front of a computer screen, and average time spent outdoors is quickly decreasing. In the same way our technology is continuously engineered and altered throughout the years, so have our lifestyles. Because of this, the fifth tenet of the "Critical Engineering Manifesto" rings true.

yuvian-lookingoutwards01

As a preface, I did not know of many interactive/computational artworks before this class and most of my exposure to this field has been from looking through OpenProcessing.

One project I remember distinctly is Jason Labbe's sketch entitled "Frozen Brush"

The user interacts with this sketch by moving their mouse across the screen, dragging the "frozen brush" along with it.

Jason Labbe is an artist with a strong background in visual effects, game development, and 3d animation. He has worked on films such as "Avatar", "The Avengers: Age of Ultron", and other projects that require the use of sophisticated special effects. Thus, one can assume that he is inspired by game engine physics and other aspects of computer-generated simulations.

Before coming across this project, I had just begun experimenting with Processing and P5, playing around with simple blocks and shapes. It was only after seeing this project and those similar to it that I realized how dynamic, intelligent, artistic, and interactive computational artworks could be. I admire the colors within this sketch and the fluidity of the movement of the "ice" as your mouse interacts with the code. Although simplistic, I think that this sketch is really beautiful because it's straightforward but also seems well-thought out. I aspire to make computational artwork that seems a lot simpler than it is while maintaining a level of artistic complexity.

One thing I would have liked to see in this project is -surprisingly- more interactivity. It would have been interesting to take in the pressure of the user's mouseclick and use that information to affect the movement of the brush. In addition, since it is titled "Frozen Brush", I would have enabled a function that allows the user to actually paint onto the screen. Another feature that would have made this project more interesting and interactive is the use of sound. For some reason, I naturally associated the movement of the brush with sound. An implementation of the visual effects of this project with another associating the position of the brush with sound would be very interesting to interact with.

yuvian-Intersections

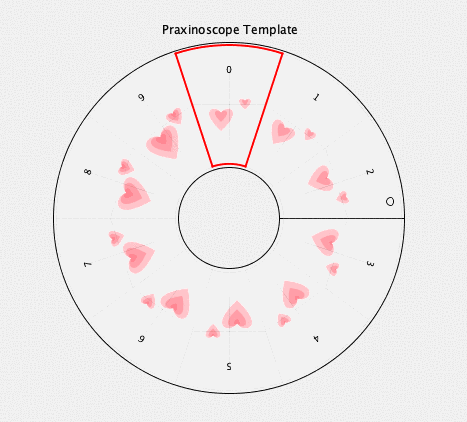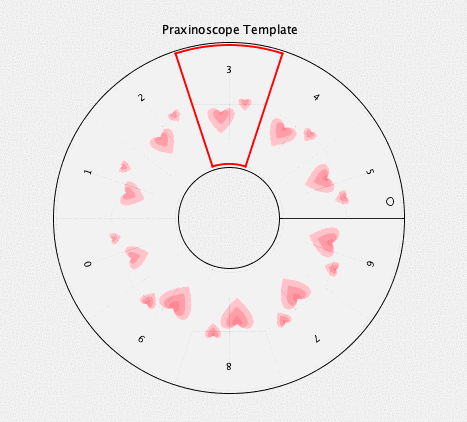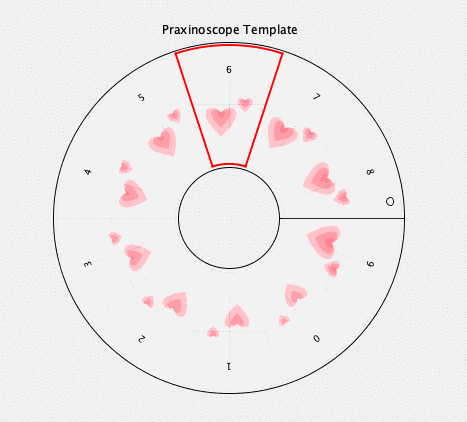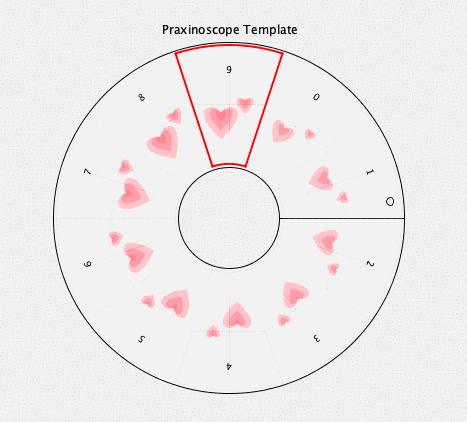
intersections

twelve intersections

seventy intersections


var lines = [];
var numOfLines = 12;
var intersectXArray =[];
var intersectYArray = [];

var yAxis = 1;
var c1, c2, c3;

function setup() {
	createCanvas(720, 480);
	
	background(0);

  c1 = color(0);
  c2 = color(16, 45, 117);
	c3 = color(244, 89, 66);
	
	// gradient background 1
	setGradient(0, 0, windowWidth, windowHeight / 2, c1, c2, yAxis);
	
	// gradient background 2
	setGradient(0, windowHeight/2, windowWidth, windowHeight, c2, c3, yAxis);
	
  for (var i = 0; i < numOfLines; i++) {
    lines.push(new Line());
  }

}

function draw() {
  for (var i = 0; i < lines.length; i++) {
    lines[i].display();
  }
  
  for (var i = 0; i < lines.length; i++) {
    for (var j = 0; j < lines.length; j++) {
      intersectXArray.push(intersect(lines[i].x1, lines[i].y1, lines[i].x2, lines[i].y2, lines[j].x1, lines[j].y1, lines[j].x2, lines[j].y2).x);
      intersectYArray.push(intersect(lines[i].x1, lines[i].y1, lines[i].x2, lines[i].y2, lines[j].x1, lines[j].y1, lines[j].x2, lines[j].y2).y);
    } 
  }  
	  
	// display twinkling stars as intersection points
  for (var i = 0; i < intersectXArray.length; i++) {
		star = new Star(intersectXArray[i], intersectYArray[i]);
		star.display();
		star.twinkle();
  }
}

function mousePressed() {
  lines = [];
  intersectXArray = [];
  intersectYArray = [];
  setup();
}

function Line() {
  this.x1 = random(0, width);
  this.y1 = random(0, height);
  this.x2 = random(0, width);
  this.y2 = random(0, height);

  this.display = function() {
    stroke(249, 252, 232, 20);
    strokeWeight(1);
    line(this.x1, this.y1, this.x2, this.y2);
  }
}

function Star(x,y) {
	this.x = x;
	this.y = y
	this.r = random(8);
	
	this.display = function() {
		stroke(22, 71, 119);
		fill(255);
		this.rc = constrain(this.r, 0, 9);
    ellipse(this.x, this.y, this.rc, this.rc);
  };

	this.twinkle = function() {
		if (this.r < 3) {
			this.r += random(-.5,1.5);
		} else if (this.r >= 3 && this.r < 6) {
			this.r += random(-1,1);
		} else if (this.r >=6 && this.r <=9) {
			this.r += random(-1.5,0.5);
		}
		
	}
}

// creates gradients
function setGradient(x, y, w, h, c1, c2, axis) {
	noFill();
	if (axis == yAxis) {  // Top to bottom gradient
   	for (var i = y; i <= y+h; i++) {
    	var inter = map(i, y, y+h, 0, 1);
    	var c = lerpColor(c1, c2, inter);
    	stroke(c);
    	line(x, i, x+w, i);
   	}
 	} 
}

//from Paul Bourke http://paulbourke.net/geometry/pointlineplane/javascript.txt
function intersect(x1, y1, x2, y2, x3, y3, x4, y4) {

  // Check if none of the lines are of length 0
  if ((x1 === x2 && y1 === y2) || (x3 === x4 && y3 === y4)) {
    return false
  }

  denominator = ((y4 - y3) * (x2 - x1) - (x4 - x3) * (y2 - y1))

  // Lines are parallel
  if (denominator === 0) {
    return false;
  }

  let ua = ((x4 - x3) * (y1 - y3) - (y4 - y3) * (x1 - x3)) / denominator;
  let ub = ((x2 - x1) * (y1 - y3) - (y2 - y1) * (x1 - x3)) / denominator;

  // is the intersection along the segments
  if (ua < 0 || ua > 1 || ub < 0 || ub > 1) {
    return false
  }

  // Return a object with the x and y coordinates of the intersection
  let x = x1 + ua * (x2 - x1)
  let y = y1 + ua * (y2 - y1)

  return {x, y}
}

yuvian-IterationExercise

var canvasWidth = 500;
var canvasHeight = canvasWidth;
var sideLength = canvasWidth/8 - 10;

function setup() {
  var bg_color = color(17, 22, 158);
  background(bg_color);
  createCanvas(canvasWidth,canvasHeight);
  noStroke();
	
  for (var x = 0; x < 8; x++) {
    for (var y = 0; y < 8; y++) {
    fill(random(50,170),random(130,200), random(230,255));
    rect(x*canvasWidth/8,y*canvasWidth/8,sideLength,sideLength);
    }
  }
}

function draw() {
  var bg_color = color(17, 22, 158);
  rectMode(CORNER);
  ellipseMode(CORNER);

  for (var x = 0; x < 8; x++) { 
    for (var y = 0; y < 8; y++) {
      var chance = random(0,1);   
      if (mouseIsPressed) {
        if (chance < 0.05 ) {
          noStroke();
          fill(bg_color);
          rect(x*canvasWidth/8, y*canvasWidth/8, canvasWidth/8, canvasWidth/8);
	  //circles are bright red
	  fill(255, 43, 92);
          ellipse(x*canvasWidth/8+3,y*canvasWidth/8+3,sideLength-3, sideLength-3);
        } else {
	  noStroke();
	  //squares lean blue
	  fill(random(50,170),random(130,200), random(230,255));
          rect(x*canvasWidth/8,y*canvasWidth/8,sideLength,sideLength); 
        } 
      }
    }
  }
}