spoon – Page 3 – 60212: INTERACTIVITY & COMPUTATION

Spoon-Interruptions

  var boolDoRefresh;
  const CANV_HEIGHT = 720;
  const CANV_WIDTH = 720;
  const H_MARGIN = CANV_WIDTH / 14;
  const V_MARGIN = CANV_HEIGHT / 14;
  const V_NUM_LINES = 56;
  const H_NUM_LINES = 56;
  const H_UNIT_SIZE = (CANV_WIDTH - (H_MARGIN * 2)) / H_NUM_LINES;
  const V_UNIT_SIZE = (CANV_HEIGHT - (V_MARGIN * 2)) / V_NUM_LINES;
  const LINE_LENGTH = H_UNIT_SIZE * 2;
  const HORIZONTAL_FREQ = 0.25;
 
  function setup() {
    createCanvas(720, 720);
    background('#EEEEEE');
    strokeWeight(0.75);
    boolDoRefresh = true;
  }
 
  function draw() {
    if(boolDoRefresh) {
      background('#EEEEEE');
      constructLines();
      boolDoRefresh = false;
    }
  }
 
  function mousePressed() {
    boolDoRefresh = true;
  }
 
  function constructLines() {
    var angleOff = random(0.2);
    var gapX = random(0.5);
    var gapY = random(0.5);
    var gapScale = 0.15;
    noiseSeed(random(100));
    var horizontal = random(1);
    for(var i = 0; i < H_NUM_LINES; i++) {
      for(var j = 0; j < V_NUM_LINES; j++) {
        angleOff += 0.1;
        gapX += i * gapScale;
        gapY += j * gapScale;
        if(noise((i * gapScale), (j * gapScale)) > 0.25) {
          var angle = random(noise(angleOff) * 90);
          centerLine(H_MARGIN + i * H_UNIT_SIZE, V_MARGIN + j * V_UNIT_SIZE, LINE_LENGTH, angle, horizontal);
        }
      }
    }
  }
 
  function centerLine(x, y, length, angle, horizontal) {
    angleMode(DEGREES);
    var randNum = random(2);
    var x1 = x + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? cos(angle) : sin(angle)));
    var y1 = y + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? sin(angle) : cos(angle)) * (randNum > 1 ? 1 : -1));
    var x2 = x - ((length / 2) * (horizontal < HORIZONTAL_FREQ ? cos(angle) : sin(angle)));
    var y2 = y + ((length / 2) * (horizontal < HORIZONTAL_FREQ ? sin(angle) : cos(angle)) * (randNum > 1 ? -1 : 1));
    line(x1, y1, x2, y2);
  }

Process/Reflection:

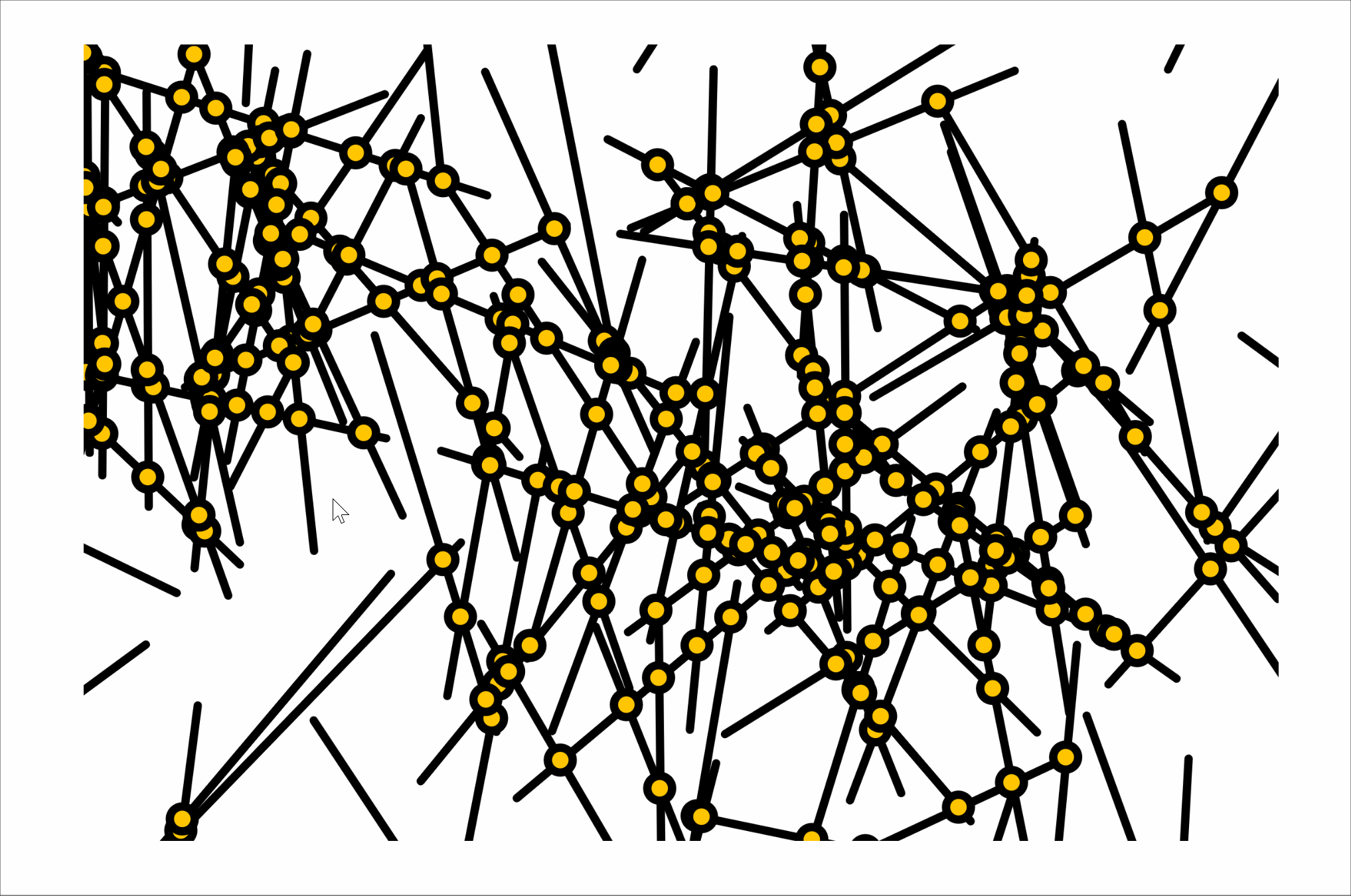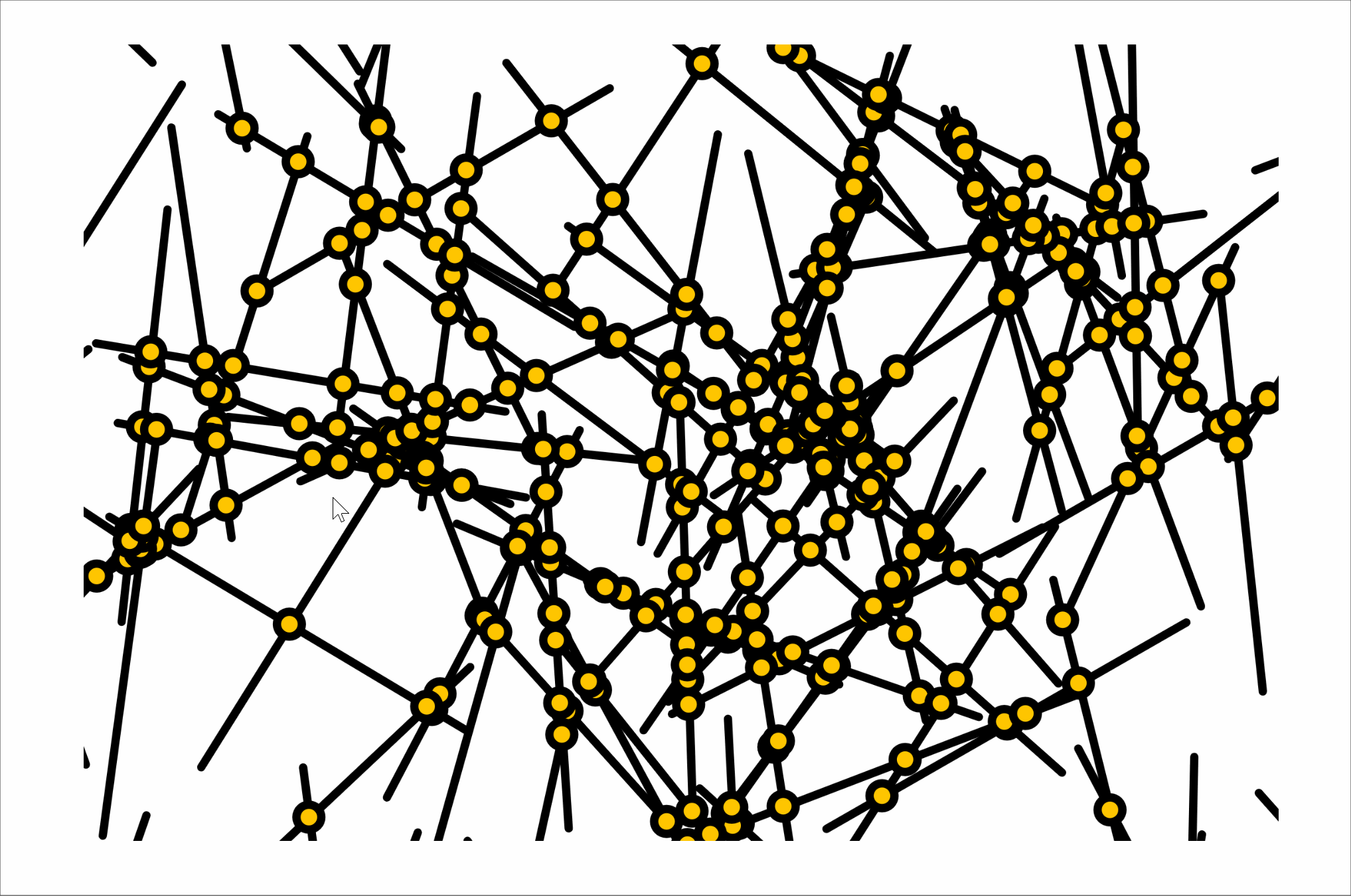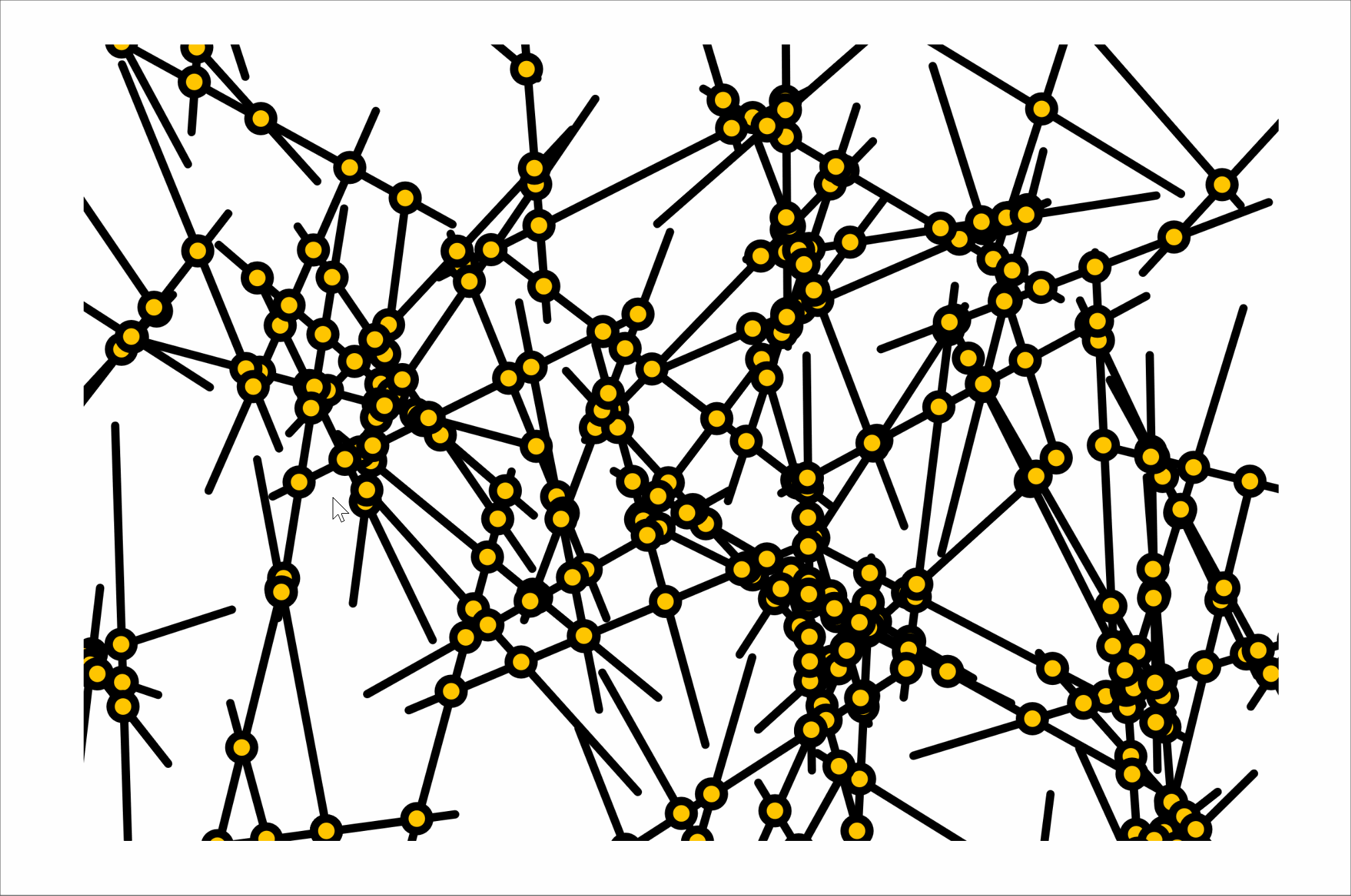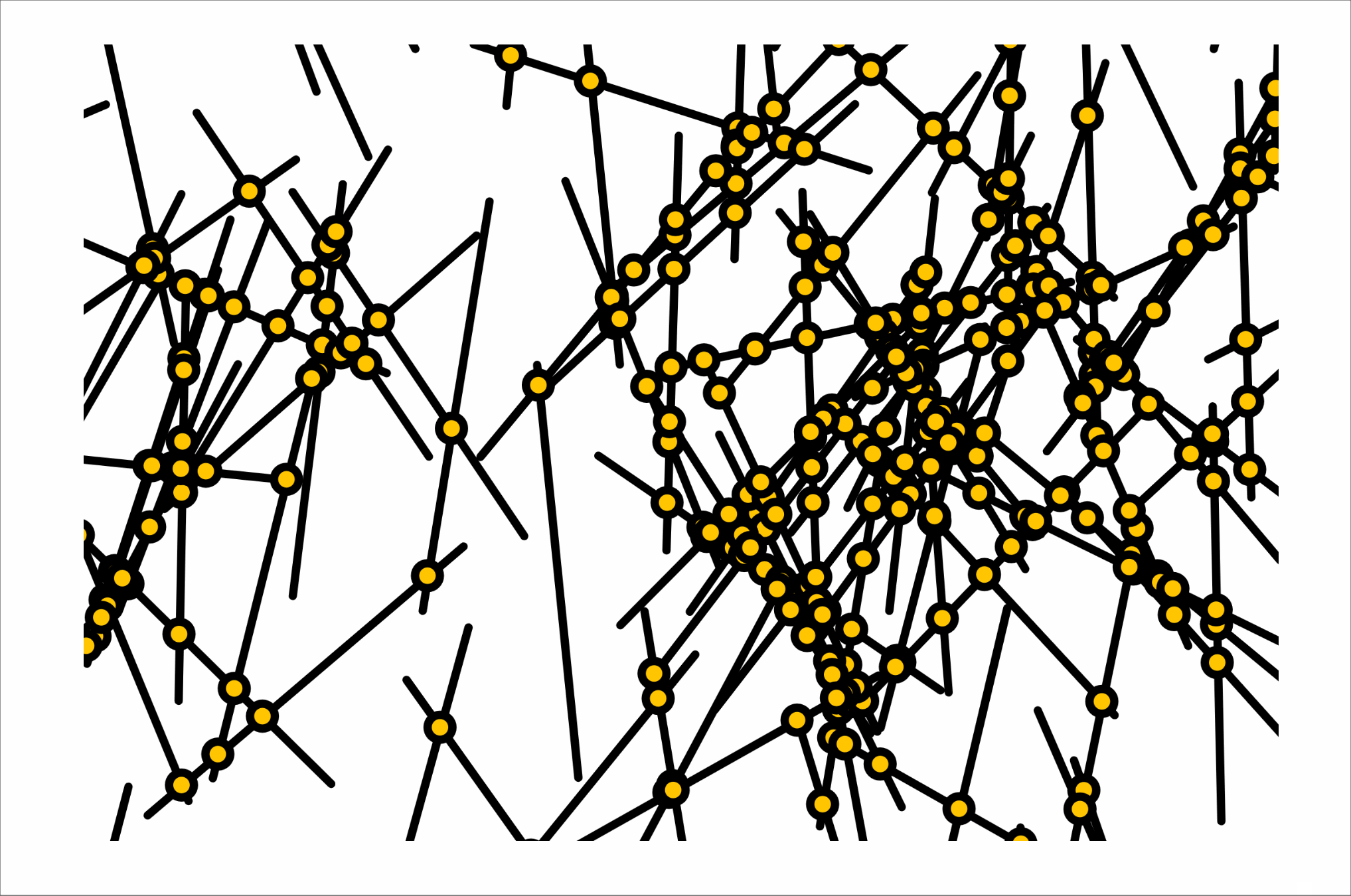
I dedicated a significant amount of my work on this project to my observations of Vera Molnár's Interruptions. I noted the following:

In each composition, all the lines are the same length.
Each line's center falls into a 56x56 grid.
Each line's length is twice the distance of the spacing on the grid (in other words, the endpoints of a fully vertical or horizontal line will intersect with the centerpoints of the lines immediately next to it)
While the lines' angles are random, they tend to point in a vertical direction on three of Molnár's compositions and in a horizontal direction on one composition
Not every line is present. There are gaps in each composition. While the location of the gaps seem random, missing lines tend to exist near other missing lines.
Gaps appear fairly infrequently
There is some slight variation in the background color, ranging from off-white to a mid-light grey.
There is a margin around each composition. Not all of the compositions are centered, but the most centered composition leaves a margin of about 1/14th of the page around the composition.

As I was creating my own compositions in Javascript, I noticed that there was a considerable amount of care needed to produce a convincing randomness. I Perlin noise to create the gaps and the variation in line angles, something that did not exist in the time when the original compositions were created, to make a composition that was close to Molnár's. I think I was only mildly successful, though, as while the lines seem to have a similar character to the originals, the gaps do not. Their borders are too harsh and they are not quite the right shape. I think my line weight is a little off, as well.

Reproducing randomness is incredibly challenging without knowledge of the calculations that led to Molnár's compositions, and I now have a much greater appreciation for the work that goes into producing art with randomness as a factor.

Spoon-Intersections

Intersections with 12 lines.

Intersections with 100 lines

 var boolDoRefresh;
 const NUM_LINES = 12;
 
 function setup() {
   createCanvas(720, 480);
   background('#FFFFFF');
   strokeWeight(5);
   boolDoRefresh = true;
 }
 
 function draw() {
   if(boolDoRefresh) {
     background('#FFFFFF');
     var lines = constructLines();
     findIntersections(lines);
     boolDoRefresh = false;
   }
 }
 
 function mousePressed() {
    boolDoRefresh = true;
 }
 
 function constructLines() {
   const LINE_LENGTH = 250;
   var lines = [];
   for(var i = 0; i < NUM_LINES; i++) {
     var x1 = random(720);
     var y1 = random(480);
     var x2 = random(100) > 50 ? x1 - random(LINE_LENGTH) : x1 + random(LINE_LENGTH);
     var y2 = ((random(100) > 50 ? 1 : -1) * sqrt(sq(LINE_LENGTH) - sq(x1 - x2))) + y1;
 
     line(x1, y1, x2, y2);
     lines[i] = [x1, y1, x2, y2];
   }
   return lines;
 }
 
 function findIntersections(lines) {
   //uses calculations found at http://paulbourke.net/geometry/pointlineplane/
   //draws circles around any points where lines intersect
   for(var i = 0; i < NUM_LINES; i++) {
     for(var j = i + 1; j < NUM_LINES; j++) {
       var x1 = lines[i][0];
       var x2 = lines[i][2];
       var y1 = lines[i][1];
       var y2 = lines[i][3];
 
       var x3 = lines[j][0];
       var x4 = lines[j][2];
       var y3 = lines[j][1];
       var y4 = lines[j][3];
 
       var u1 = (((x4 - x3) * (y1 - y3)) - ((y4 - y3) * (x1 - x3)))
            / (((y4 - y3) * (x2 - x1)) - ((x4 - x3) * (y2 - y1)));
       var u2 = (((x2 - x1) * (y1 - y3)) - ((y2 - y1) * (x1 - x3)))
            / (((y4 - y3) * (x2 - x1)) - ((x4 - x3) * (y2 - y1)));
 
       if(u1 > 0 && u1 < 1 && u2 > 0 && u2 < 1) {
         var x = x1 + (u1 * (x2 - x1));
         var y = y1 + (u1 * (y2 - y1));
         fill('#FFC600');
         ellipse(x, y, 15);
       }
     }
   }
 }

Spoon-IterationExcercise

// using starter code for "Embedded Iteration + Randomness"
var boolDoRefresh;
 
function setup() {
  createCanvas(625, 625);
  strokeWeight(5);
  boolDoRefresh = true;
}
 
function draw() {
  if(boolDoRefresh) {
    for(var x = 50; x < 625; x += 75) {
      for(var y = 50; y < 625; y += 75) {
        drawItemAtPosition(x, y);
      }
    }
    boolDoRefresh = false;
  }
}
 
function mousePressed() {
  boolDoRefresh = true;
}
 
function drawItemAtPosition(x, y) {
  //draws an item with a center on the position given.
  var drawYellow = random(255) > 235;
  if(drawYellow) fill('#FFC600');
  else fill('#FFFFFF');
  rect(x - 25, y - 25, 50, 50);
}