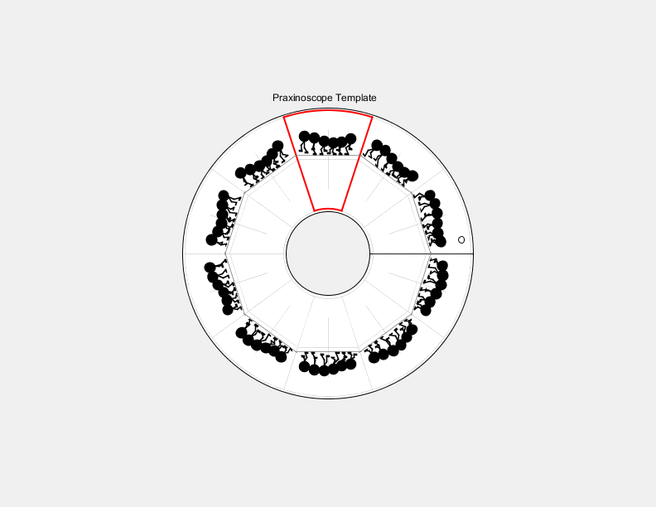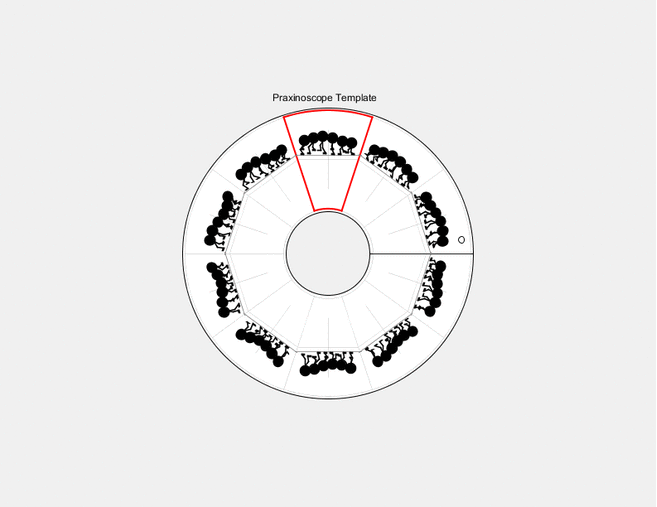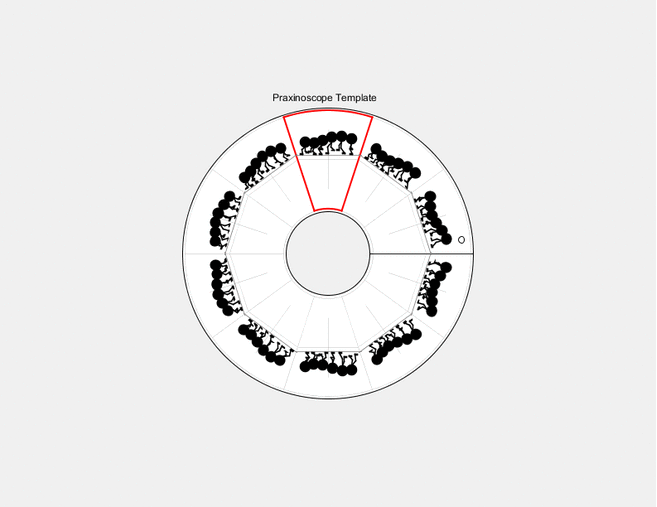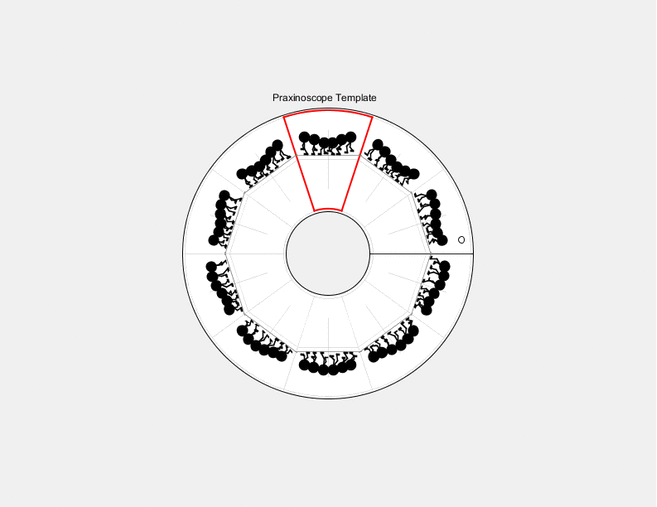
// This is a template for creating a looping animation in Processing/Java.
// When you press the 'F' key, this program will export a series of images
// into a "frames" directory located in its sketch folder.
// These can then be combined into an animated gif.
// Known to work with Processing 3.3.6
// Prof. Golan Levin, January 2018
//===================================================
// Global variables.
String myNickname = "dinkolas";
int nFramesInLoop = 120;
int nElapsedFrames;
boolean bRecording;
//===================================================
void setup() {
size (640,640);
bRecording = true;
nElapsedFrames = 0;
}
//===================================================
void keyPressed() {
if ((key == 'f') || (key == 'F')) {
bRecording = true;
nElapsedFrames = 0;
}
}
//===================================================
void draw() {
// Compute a percentage (0...1) representing where we are in the loop.
float percentCompleteFraction = 0;
if (bRecording) {
percentCompleteFraction = (float) nElapsedFrames / (float)nFramesInLoop;
} else {
percentCompleteFraction = (float) (frameCount % nFramesInLoop) / (float)nFramesInLoop;
}
// Render the design, based on that percentage.
renderMyDesign (percentCompleteFraction);
// If we're recording the output, save the frame to a file.
if (bRecording) {
saveFrame("frames/" + myNickname + "_frame_" + nf(nElapsedFrames, 4) + ".png");
nElapsedFrames++;
if (nElapsedFrames >= nFramesInLoop) {
bRecording = false;
}
}
}
//===================================================
void renderMyDesign (float percent) {
color c1 = color(59,58,133);
color c2 = color(137,52,109);
color c3 = color(199,96,88);
color c4 = color(255,178,72);
color c5 = color(255,225,150);
background(c5);
//1
color bodyCol = c3;
color legCol = c2;
float originX = 100;
float originY = 200;
float xShift = -20;
float altitude = 100;
float diameter = 70;
float bounce = 10;
float legLength = 50;
float legWeight = 10;
float footLength = 10;
float cycles = 2;
float footH = 40;
float footV = 20;
float phase = 0;
float legT = function_DoubleExponentialSigmoid(percent,.5);
float bodyT = function_DoubleExponentialSigmoid(percent,.5);
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
//2
bodyCol = c1;
legCol = c2;
originX = 320;
originY = 190;
xShift = 10;
altitude = 90;
diameter = 120;
bounce = 5;
legLength = 25;
legWeight = 15;
footLength = 10;
cycles = 1;
footH = 20;
footV = 10;
phase = .5;
legT = function_ExponentialSmoothedStaircase(percent,.05,4);
bodyT = legT;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
//3
bodyCol = c4;
legCol = c3;
originX = 520;
originY = 250;
xShift = 0;
altitude = 200;
diameter = 50;
bounce = 15;
legLength = 100;
legWeight = 8;
footLength = 10;
cycles = 3;
footH = 30;
footV = 60;
phase = .6;
legT = 1-percent;
bodyT = 1-percent;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
//4
for (int i = 0; i < 3; i++){
bodyCol = c3;
legCol = c1;
originX = 50+55*i;
originY = 350;
xShift = 0;
altitude = 40;
diameter = 40;
bounce = 3;
legLength = 20;
legWeight = 4;
footLength = 3;
cycles = 2;
footH = 10;
footV = 6;
phase = .1+.3*i;
legT = function_AdjustableCenterEllipticWindow (percent, .5);
bodyT = percent;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
}
//5
bodyCol = c3;
legCol = c1;
originX = 490;
originY = 430;
xShift = 10;
altitude = 90;
diameter = 50;
bounce = 15;
legLength = 60;
legWeight = 8;
footLength = 10;
cycles = 1;
footH = 80;
footV = 130;
phase = .6;
legT = percent;
bodyT = percent;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
//6
bodyCol = c3;
legCol = c4;
originX = 300;
originY = 380;
xShift = -30;
altitude = 100;
diameter = 60;
bounce = 25;
legLength = 40;
legWeight = 10;
footLength = 10;
cycles = 2;
footH = 40;
footV = 40;
phase = .8;
legT = 2*function_CircularEaseInOut(percent);
bodyT = percent;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
//7
bodyCol = c1;
legCol = c4;
originX = 400;
originY = 600;
xShift = 0;
altitude = 70;
diameter = 30;
bounce = 5;
legLength = 60;
legWeight = 10;
footLength = 5;
cycles = 1;
footH = 120;
footV = 35;
phase = 0;
legT = percent;
bodyT = 1-percent;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
//8
bodyCol = c2;
legCol = c4;
originX = 100;
originY = 580;
xShift = 20;
altitude = 130;
diameter = 70;
bounce = 40;
legLength = 70;
legWeight = 20;
footLength = 30;
cycles = 2;
footH = 30;
footV = 35;
phase = .5;
legT = percent;
bodyT = 1-percent;
drawCharacter(bodyCol, legCol, originX, originY, xShift, altitude, diameter, bounce, legLength, legWeight, footLength, cycles, footH, footV, phase, legT, bodyT);
}
void drawCharacter(color bodyCol, color legCol, float originX, float originY, float xShift, float altitude, float diameter, float bounce, float legLength, float legWeight, float footLength, float cycles, float footH, float footV, float phase, float legT, float bodyT) {
//set origin and coordinate system so up is positive
translate(originX,originY);
scale(1,-1);
legT = ((legT%(1/cycles))*cycles+phase)%1;
bodyT = ((bodyT%(1/cycles/2))*2*cycles+phase)%1;
stroke(bodyCol);
strokeWeight(legWeight);
line(-footH-20,-legWeight/2,footH+20+footLength,-legWeight/2);
//body positions
float bodyX = xShift+map(-sin(TWO_PI*bodyT), -1,1, -bounce/5, +bounce/5);
float bodyY = map(-cos(TWO_PI*bodyT), -1,1, altitude-bounce, altitude+bounce);
//back leg
//hip=(x1,y1), ankle=(x2,y2), knee = (a,b), toe = (x3,y3)
translate(0,legWeight/2);
strokeWeight(legWeight);
stroke(legCol);
noFill();
float x1 = bodyX;
float y1 = bodyY-diameter/3;
float x2 = map(-cos(TWO_PI*legT), -1,1,-footH,footH);
float y2 = max(0,map(sin(TWO_PI*legT), -1, 1, -footV, footV));
float mult = -.5*sqrt(4*pow(legLength,2)/(pow(x2-x1,2)+pow(y2-y1,2))-1);
float a = .5*(x1+x2)+mult*(y2-y1);
float b = .5*(y1+y2)+mult*(x1-x2);
float x3 = x2 + footLength;
float y3 = 0;
if (2*legLength < sqrt(pow(x2-x1,2)+pow(y2-y1,2))){line(x1,y1,x2,y2);}
else{line(x1,y1,a,b);line(a,b,x2,y2);}
if (y2==0) {line(x2,y2,x3,y3);}
else {
float angle = atan((y2-y1)/(x2-x1));
angle = PI/2-angle;
if (x2<x1) {angle+=PI;}
translate(x2,y2);
rotate(-angle);
line(0,0,-footLength,0);
rotate(angle);
translate(-x2,-y2);
}
translate(0,-legWeight/2);
//body
noStroke();
fill(bodyCol);
ellipse(bodyX,bodyY,diameter,diameter);
//front leg
//hip=(x1,y1), ankle=(x2,y2), knee = (a,b), toe = (x3,y3)
legT = (legT+.5)%1;
translate(0,legWeight/2);
strokeWeight(legWeight);
stroke(legCol);
x1 = bodyX;
y1 = bodyY-diameter/3;
x2 = map(-cos(TWO_PI*legT), -1,1,-footH,footH);
y2 = max(0,map(sin(TWO_PI*legT), -1, 1, -footV, footV));
mult = -.5*sqrt(4*pow(legLength,2)/(pow(x2-x1,2)+pow(y2-y1,2))-1);
a = .5*(x1+x2)+mult*(y2-y1);
b = .5*(y1+y2)+mult*(x1-x2);
x3 = x2 + footLength;
y3 = 0;
if (2*legLength < sqrt(pow(x2-x1,2)+pow(y2-y1,2))){line(x1,y1,x2,y2);}
else{line(x1,y1,a,b);line(a,b,x2,y2);}
if (y2==0) {line(x2,y2,x3,y3);}
else {
float angle = atan((y2-y1)/(x2-x1));
angle = PI/2-angle;
if (x2<x1) {angle+=PI;}
translate(x2,y2);
rotate(-angle);
line(0,0,-footLength,0);
rotate(angle);
translate(-x2,-y2);
}
translate(0,-legWeight/2);
//reset origin
scale(1,-1);
translate(-originX,-originY);
}
//===================================================
// Taken from https://github.com/golanlevin/Pattern_Master
float function_DoubleExponentialSigmoid (float x, float a) {
// functionName = "Double-Exponential Sigmoid";
float min_param_a = 0.0 + EPSILON;
float max_param_a = 1.0 - EPSILON;
a = constrain(a, min_param_a, max_param_a);
a = 1-a;
float y = 0;
if (x<=0.5) {
y = (pow(2.0*x, 1.0/a))/2.0;
} else {
y = 1.0 - (pow(2.0*(1.0-x), 1.0/a))/2.0;
}
return y;
}
float function_ExponentialSmoothedStaircase (float x, float a, int n) {
//functionName = "Smoothed Exponential Staircase";
// See http://web.mit.edu/fnl/volume/204/winston.html
float fa = sq (map(a, 0,1, 5,30));
float y = 0;
for (int i=0; i<n; i++){
y += (1.0/(n-1.0))/ (1.0 + exp(fa*(((i+1.0)/n) - x)));
}
y = constrain(y, 0,1);
return y;
}
float function_AdjustableCenterEllipticWindow (float x, float a){
//functionName = "Adjustable-Center Elliptic Window";
float min_param_a = 0.0 + EPSILON;
float max_param_a = 1.0 - EPSILON;
a = constrain(a, min_param_a, max_param_a);
float y = 0;
if (x<=a){
y = (1.0/a) * sqrt(sq(a) - sq(x-a));
}
else {
y = (1.0/(1-a)) * sqrt(sq(1.0-a) - sq(x-a));
}
return y;
}
float function_CircularEaseInOut (float x) {
//functionName = "Penner's Circular Ease InOut";
float y = 0;
x *= 2.0;
if (x < 1) {
y = -0.5 * (sqrt(1.0 - x*x) - 1.0);
} else {
x -= 2.0;
y = 0.5 * (sqrt(1.0 - x*x) + 1.0);
}
return y;
} |