02-24 Movement

Agenda

Movement: Frame-Based

I. We can use the p5.js frameCount variable to govern a visual property, such as the position of a circle. Note how the frameCount increases without bound over time; to re-set the sketch, click the circular button in the top center (sketch):

II. Here, a global variable (declared outside of setup or draw) is incremented each frame, and reset when it exceeds a certain number (sketch):

III. Note that your app’s frame rate will affect the apparent speed (in pixels per second) of such animation. For example, if your app is calculating a lot of math on every frame, each frame will take longer, the frame rate will drop, and the animation will appear slower. This can also happen if you adjust the frame rate directly (sketch):

IV. That’s a crude way to adjust the speed (and not recommended!). Instead, we can use a global variable, increased by a “speed” variable on each frame, and reset when it exceeds a certain number (sketch):

V. We can combine the above type of animation with some if blocks to make a bouncing ball. If the ball’s position exceeds the bounds of the canvas, we reverse its speed in that direction (sketch):

Movement: Time-Based

VI. We can use the p5.js millis() command to access the number of milliseconds since the sketch started. Note that this increases without bounds, and also note that it increases “quickly” (by 1000 units per second!). Here, I’ve divided the millis by 10.0 so you can see the animation more slowly (sketch):

VII. With the millis(), since the animation is now governed by absolute clock time, the “speed” of objects as they move across the screen (in pixels per second) is no longer affected by frame rate. Instead, altering the frame rate simply makes the animation look smoother or choppier (sketch):

The GIF below helps explain this effect. The text graphics are all moving at the same speed, but they’re moving with different frame rates:

VIII. It’s problematic to link a position or other visual property to the millis(), because this value increases forever. One trick to keep values in a usable range is to use the modulo operator (%), which returns the remainder of a number after division. In this sketch, the position is based on the “millis() mod the width” (sketch):

If you’d like to learn more about how to understand or use the modulo operator, I gave a guest lecture about this on the Coding Train:

IX. Here, I’ve rearranged the terms slightly to produce a loop with a precisely-known duration. Note how I have calculated a variable, percentOfLoop, which represents our progress through the current loop as a number between 0 and 1. That’s an incredibly useful number! (sketch):

X. Percentages (i.e. numbers in the range between zero and one) have some special properties that make them especially useful for animation. One common trick is to raise them to a power (using the pow() command); this produces altered (non-linear) types of movement—like “ease-in” and “ease-out”—as in the following diagram.

Raising a percentage to a number higher than 1 (like 2.0) produces an ease-in animation, while raising a percentage to a fraction (like 0.5) produces an ease-out animation. You can see that in the following (sketch):

(Note how they all begin and end at the same moment! That’s because the endpoint values of 0 and 1 are unaffected by the power function.)

We will be using an add-on library (p5.createloop) to help create a looping structure for us. You can see the code for this sketch here:

Circular Movement

Let’s recall what a “sine wave” is.  It is a smoothly varying, periodic curve that represents the vertical position of a point on a unit circle, as a function of the angle of the radius that touches that point:

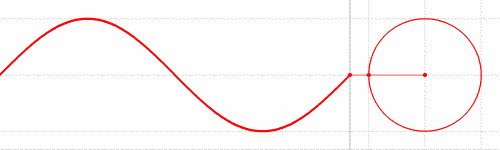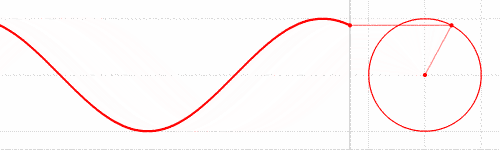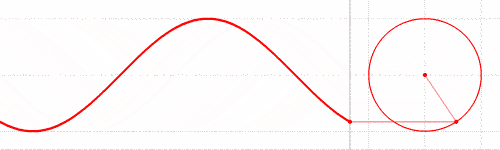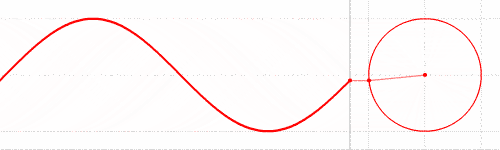
Often that angle is called theta (θ), and we typically sweep theta from 0 through 2π radians (equivalent to 360°). We can also look at the horizontal position of the point on the unit circle — it generates the very similar cosine curve (blue in the diagram below):

Sinusoidal movement (sketch):

Apps to do:

  • Sine wave
  • Generate a circle
  • Generate circles 1x,2x,3x
  • Lissajous figures