Summary: A graphical representation of lambda calculus
Abstract: Lambda calculus is typically presented in computer science as that strange other way of think about computing, complete with an impenetrable syntax and little to no metaphor. GraphLambda seeks to overcome these limitations by presenting lambda calculus in a graphical rather than textual format.
Repository: https://github.com/scgruber/GraphLambda
Lambda Calculus: it’s that strange, other way of thinking about computation. Rather than coupling computer programs to a physical machine, we can look at them as pure mathematical functions. This should be simple, easier to understand even than a Turing Machine. And yet, trying to learn Lambda Calculus means subjecting yourself to an endless barrage of this:
GREP := Y(\gfx.NULLxNIL(f(CARx)(PAIR(CARx))I(gf(CDRx))))
GCD := (\gmn.LEmn(gnm)(gmn))(Y(\gxy.ISZEROyx(gy(MODxy))))
There should be an easier way. And there is.
Lambda calculus operates entirely by function-objects acting on other function-objects. It operates in parallel as much as it possibly can. And it doesn’t depend on any structured naming conventions. For all of these reasons, it is a natural fit for a graphical representation of the program structure. By turning garbled string of textual lambda calculus into a pictorial form, we are able to harness the brain’s innate strengths of image processing in order to improve the readability of this underappreciated model of computing.
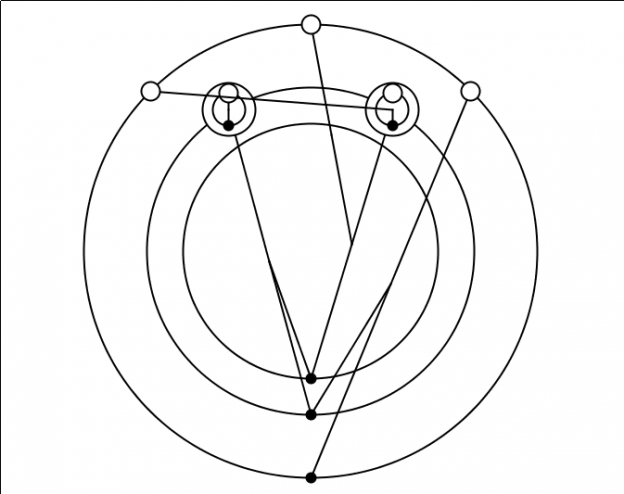
GraphLambda presents lambda calculus programs in a graphical view, using a simple vocabulary of relationships between nodes. Open circles denote inputs, which may have been pre-filled with lambda expressions or left empty. Closed circles denote the output of abstractions. Variable applications and duplications are indicated by branching and recombining paths in the diagram. Editing is currently possible by typing to alter the lambda expression that is currently active.
Immediate improvements that I would like to make include resolving unnecessary or confusing path crossings in the diagram and topologically sorting the branch and application paths for clarity. In the long term, I would like to implement a native graphical editor for building lambda programs.